Dirac-Feynman-Berezin amplitudes 3 - Electromagnetism

By Chris Austin. 28 November 2020.

An earlier version of this post was published on another website on 13 October 2012.

This is the third part of a ten-part post on the foundation of our understanding of high energy physics, which is Richard Feynman's functional integral. The first two parts are Action and Multiple Molecules, and the following parts, which will appear at intervals of about a month, are Action for Fields, Radiation in an Oven, Matrix Multiplication, The Functional Integral, Gauge Invariance, Photons, and Interactions.

I'm hoping this blog will be fun and useful for everyone with an interest in science, so although I'll pop up a few formulae again, I'll still try to keep them friendly by explaining all the pieces, as in the first two parts of the post. Please feel free to ask a question in the Comments, if you think anything in the post is unclear.

The clue that led to the discovery of quantum mechanics, whose principles are summarized in Feynman's functional integral, came from the attempted application to electromagnetic radiation of discoveries about heat and temperature. We looked at those discoveries about heat and temperature in the second part of the post, and today I would like to show you how James Clerk Maxwell, just after the middle of the nineteenth century, was able to identify light as waves of oscillating electric and magnetic fields, and to calculate the speed of light from measurements of:

the force between parallel wires carrying electric currents;
the heat given off by a long thin wire carrying an electric current; and
the time integral of the temporary electric current that flows through a long thin wire, when a voltage is introduced between two parallel metal plates, close to each other but not touching, via that wire.

In addition to his work on the distribution of energy among the molecules in a gas, which we looked at in the second part of the post, Maxwell summarized the existing knowledge about electricity and magnetism into equations now called Maxwell's equations, and after identifying and correcting a logical inconsistency in these equations, he showed that they implied the possible existence of waves of oscillating electric and magnetic fields, whose speed of propagation would be equal within observational errors to the speed of light, which was roughly known from Olaf Romer's observation, made around 1676, of a 16 minute time lag between the motions of Jupiter's moons as seen from Earth on the far side of the Sun from Jupiter, and as seen from Earth on the same side of the Sun as Jupiter, together with the distance from the Earth to the Sun, which was roughly known from simultaneous observations of Mars in 1672 from opposite sides of the Atlantic by Giovanni Domenico Cassini and Jean Richer, and observations of the transit of Venus. The speed of light had also been measured in the laboratory by Hippolyte Fizeau in 1849, and more accurately by Léon Foucault in 1862. Maxwell therefore suggested that light was electromagnetic radiation, and that electromagnetic radiation of wavelengths outside the visible range, which from Thomas Young's experiments with double slits was known to comprise wavelengths between about $4 \times 10^{- 7}$ metres for violet light and $7 \times 10^{- 7}$ metres for red light, would also exist. This was the other part of the clue that led to the discovery of quantum mechanics and Feynman's functional integral.

In his writings around 600 BC, Thales of Miletus described how amber attracts light objects after it is rubbed. The Greek word for amber is elektron, which has been adapted to the English word electron, for the first of the elementary matter particles of the Standard Model to be discovered. Benjamin Franklin and Sir William Watson suggested in 1746 that the two types of static electricity, known as vitreous and resinous, corresponded to a surplus and a deficiency of a single "electrical fluid" present in all matter, whose total amount was conserved. Matter with a surplus of the fluid was referred to as "positively" charged, and matter with a deficiency of the fluid was referred to as "negatively" charged. Objects with the same sign of charge repelled each other, and objects with opposite sign of charge attracted each other. Around 1766, Joseph Priestley suggested that the strength of the force between electrostatic charges is inversely proportional to the square of the distance between them, and this was approximately experimentally verified in 1785 by Charles-Augustin de Coulomb, who also showed that the strength of the force between two charges is proportional to the product of the charges.

Most things in the everyday world have no net electric charge, because the charges of the positively and negatively charged particles they contain cancel out. In particular, a wire carrying an electric current usually has no net electric charge, because the charges of the moving particles that produce the current are cancelled by the opposite charges of particles that can vibrate about their average positions, but have no net movement in any direction.

Jean-Baptiste Biot and Félix Savart discovered in 1820 that a steady electric current in a long straight wire produces a magnetic field in the region around the wire, whose direction is at every point perpendicular to the plane defined by the point and the wire, and whose magnitude is proportional to the current in the wire, and inversely proportional to the distance of the point from the wire. André-Marie Ampère discovered in 1826 that this magnetic field produces a force between two long straight parallel wires carrying electric currents, such that the force is attractive if the currents are in the same direction and repulsive if the currents are in opposite directions, and the strength of the force is proportional to the product of the currents, and inversely proportional to the distance between the wires. Thus the force on either wire is proportional to the product of the current in that wire and the magnetic field produced at the position of that wire by the other wire, and the direction of the force is perpendicular both to the magnetic field and the direction of the current.

Ampère's law is used to define both the unit of electric current, which is called the amp, and the unit of electric charge, which is called the coulomb. The amp is defined to be the electric current which, flowing along each of two very long straight parallel thin wires one metre apart in a vacuum, produces a force of $2 \times 10^{- 7}$ kilogram metres per second between them, per metre of their length. The coulomb is then defined to be the amount of moving electric charge which flows in one second through any cross-section of a wire carrying a current of one amp. Electric currents are often measured in practice by moving-coil ammeters, in which the deflection of the indicator needle is produced by letting the current flow through a movable coil suspended in the field of a permanent magnet, that has been calibrated against the magnetic field produced by a current-carrying wire.

Maxwell interpreted the force on a wire carrying an electric current in the presence of a magnetic field as being due to a force exerted by the magnetic field on the moving electric charge carriers in the wire, and defined the magnetic induction to be such that, in Cartesian coordinates, the force on a particle of electric charge moving with velocity in the magnetic field , is:

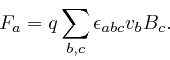
$\begin{displaymath}F_a = q \sum_{b, c} \epsilon_{a b c} v_b B_c . \end{displaymath}$

Here each index , , or can take values 1, 2, 3, corresponding to the directions in which the three Cartesian coordinates of spatial position increase. I explained the meaning of the symbol $\sum$ in the first part of the post, here. represents the collection of data that gives the value of the magnetic field in each coordinate direction at each position in space and each moment in time, so that if represents a position in space, the value of the magnetic field in coordinate direction , at position , and time , could be represented as $B_{a x t}$ or $B_a \left( x, t \right)$ , for example. If represents the collection of data that gives the particle's position at each time , then $v_c = \frac{\mathrm{d} y_a}{\mathrm{d} t}$ . represents the collection of data that gives the force on the particle in each coordinate direction at each moment in time.

The symbol $\epsilon$ is an alternative form of the Greek letter epsilon. The expression $\epsilon_{a b c}$ is defined to be 1 if the values of , , and are 1, 2, 3 or 2, 3, 1 or 3, 1, 2; if the values of , , and are 2, 1, 3 or 3, 2, 1 or 1, 3, 2; and 0 if two or more of the indexes have the same value. Thus the value of $\epsilon_{a b c}$ changes by a factor if any pair of its indexes are swapped. A quantity that depends on two or more direction indexes is called a tensor, and a quantity whose value is multiplied by if two of its indexes of the same type are swapped is said to be "antisymmetric" in those indexes. Thus $\epsilon_{a b c}$ is an example of a totally antisymmetric tensor.

A quantity that depends on position and time is called a field, and a quantity that depends on one direction index is called a vector, so the magnetic induction is an example of a vector field. From the above equation, the unit of the magnetic induction is kilograms per second per coulomb.

Since no position or time dependence is displayed in the above equation, the quantities that depend on time are all understood to be evaluated at the same time, and the equation is understood to be valid for all values of that time. The magnetic field is understood to be evaluated at the position of the particle, and the summations over and are understood to go over all the values of and for which the expressions are defined. Thus if we explicitly displayed all the indexes and the ranges of the summations, the equation could be written:

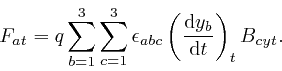
$\begin{displaymath}F_{a t} = q \sum_{b = 1}^3 \sum_{c = 1}^3 \epsilon_{a b c} \left( \frac{\mathrm{d} y_b}{\mathrm{d} t} \right)_t B_{c y t} . \end{displaymath}$

Maxwell also interpreted the electrostatic force on an electrically charged particle in the presence of another electrically charged particle as being due to a force exerted by an electric field produced by the second particle, and defined the electric field strength to be such that, in the same notation as before, the force on a particle of electric charge in the electric field , is:

$\begin{displaymath}F_a = qE_a . \end{displaymath}$

Thus the unit of the electric field strength is kilograms metres per second per coulomb, which can also be written as joules per metre per coulomb, since a joule, which is the international unit of energy, is one kilogram metre per second. The electric field strength is another example of a vector field.

Electric voltage is the electrical energy in joules per coulomb of electric charge. Thus if the electrostatic force can be derived from a potential energy by $F_a = - \frac{\partial U}{\partial x_a}$ , as in the example for which we derived Newton's second law of motion from de Maupertuis's principle, then the electric field strength is related to by $E_a = - \frac{1}{q} \frac{\partial U}{\partial x_a}$ . I have written the potential energy here as instead of , to avoid confusing it with voltage. $\frac{1}{q} U$ is the potential voltage, so the electric field strength is minus the gradient of the potential voltage, and the unit of electric field strength can also be expressed as volts per metre.

The voltage produced by a voltage source such as a battery can be measured absolutely by measuring the current that flows and the heat that is produced, when the terminals of the voltage source are connected through an electrical resistance. In all currently known electrical conductors at room temperature, an electric current flowing through the conductor quickly stops flowing due to frictional effects such as scattering of the moving charge carriers by the stationary charges in the material, unless the current is continually driven by a voltage difference between the ends of the conductor, that produces an electric field along the conductor. The work done by a voltage source of volts to move an electric charge of coulombs from one terminal of the voltage source to the other is joules, so if a current of amps coulombs per second is flowing, the work done by the voltage source per second is joules per second watts, since a watt, which is the international unit of power, is one joule per second. Thus the voltage produced by a voltage source can be measured absolutely by connecting the terminals of the voltage source by for example a long thin insulated copper wire that is coiled in a thermally insulated flask of water, and measuring the electric current and the rate at which the water temperature rises, since the specific heat capacity of water is known from measurements by James Joule to be about 4180 joules per kilogram per degree centigrade.

Maxwell summarized Coulomb's law for the electrostatic force between two stationary electric charges by the equation:

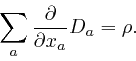
$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} D_a = \rho . \end{displaymath}$

Here is a vector field called the electric displacement, whose relation to the electric field strength at a position depends on the material present at . $\frac{\partial}{\partial x_a}$ has the same meaning as in the first part of the post, here, with now taken as , and now taken as . $\rho$ is the Greek letter rho, and represents the collection of data that gives the amount of electric charge per unit volume, at each spatial position and time . It is called the electric charge density. For each position and time , it is defined to be the amount of electric charge inside a small volume $\mathrm{d} V$ centred at , divided by $\mathrm{d} V$ , where the ratio is taken in the limit that $\mathrm{d} V$ tends to 0. A field that does not depend on any direction indexes is called a scalar field, so $\rho$ is an example of a scalar field. The units of $\rho$ are coulombs per metre, so the units of are coulombs per metre.

In most materials the electric displacement and the electric field strength are related by:

$\begin{displaymath}D = \epsilon E, \end{displaymath}$

where $\epsilon$ is a number called the permittivity of the material. Although the same symbol is used for the permittivity and the antisymmetric tensor $\epsilon_{a b c}$ , I will always show the indices on $\epsilon_{a b c}$ , so that it can't be mistaken for the permittivity.

To check that the above equation summarizing Coulomb's law leads to the inverse square law for the electrostatic force between stationary point-like charges as measured by Coulomb, we'll calculate the electric field produced by a small electrically charged sphere. We'll choose the zero of each of the three Cartesian coordinates to be at the centre of the sphere, and represent the radius of the sphere by . The electric charge per unit volume, $\rho$ , might depend on position in the sphere, for example the charge might be concentrated in a thin layer just inside the surface of the sphere. We'll assume that $\rho_x$ , the value of $\rho$ at position , does not depend on the direction from to the centre of the sphere, although it might depend on the distance $r = \sqrt{x^2_1 + x^2_2 + x^2_3}$ from to the centre of the sphere. The electric displacement at position will be directed along the straight line from to the centre of the sphere, so for , where is a quantity that depends on . From Leibniz's rule for the rate of change of a product, which we obtained in the first part of the post, here, we have:

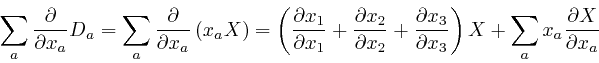
$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} D_a = \sum_a \frac{\part... ...l x_3} \right) X + \sum_a x_a \frac{\partial X}{\partial x_a} \end{displaymath}$

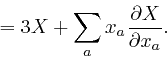
$\begin{displaymath}= 3 X + \sum_a x_a \frac{\partial X}{\partial x_a} . \end{displaymath}$

And since only depends on through the dependence of on , we have:

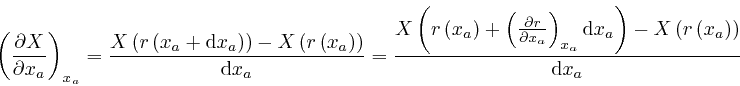
$\begin{displaymath}\left( \frac{\partial X}{\partial x_a} \right)_{x_a} = \frac{... ...ght) - X \left( r \left( x_a \right) \right)}{\mathrm{d} x_a} \end{displaymath}$

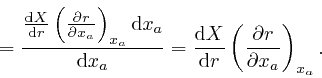
$\begin{displaymath}= \frac{\frac{\mathrm{d} X}{\mathrm{d} r} \left( \frac{\parti... ...m{d} r} \left( \frac{\partial r}{\partial x_a} \right)_{x_a} . \end{displaymath}$

The values of the components of other than are fixed throughout this formula, so their values don't need to be displayed. From this formula and the previous one:

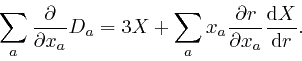
$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} D_a = 3 X + \sum_a x_a \... ...\partial r}{\partial x_a} \frac{\mathrm{d} X}{\mathrm{d} r} . \end{displaymath}$

Leibniz's rule for the rate of change of a product also gives us:

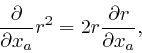
$\begin{displaymath}\frac{\partial}{\partial x_a} r^2 = 2 r \frac{\partial r}{\partial x_a}, \end{displaymath}$

and since , it also gives us:

$\begin{displaymath}\frac{\partial}{\partial x_a} r^2 = \frac{\partial}{\partial x_a} \left( x^2_1 + x^2_2 + x^2_3 \right) = 2 x_a, \end{displaymath}$

since, for example, $\frac{\partial}{\partial x_1} x^2_1 = 2 x_1$ , while $\frac{\partial}{\partial x_1} x^2_2 = \frac{\partial}{\partial x_1} x^2_3 = 0$ . Thus

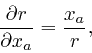
$\begin{displaymath}\frac{\partial r}{\partial x_a} = \frac{x_a}{r}, \end{displaymath}$

so from the previous formula,

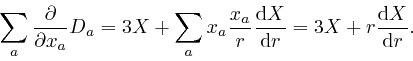
$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} D_a = 3 X + \sum_a x_a \... ...}{\mathrm{d} r} = 3 X + r \frac{\mathrm{d} X}{\mathrm{d} r} . \end{displaymath}$

Thus from Maxwell's equation summarizing Coulomb's law, above:

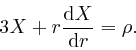
$\begin{displaymath}3 X + r \frac{\mathrm{d} X}{\mathrm{d} r} = \rho . \end{displaymath}$

From Leibniz's rule for the rate of change of a product, we have:

$\begin{displaymath}\frac{\mathrm{d}}{\mathrm{d} r} \left( r^3 X \right) = \left(... ...athrm{d} r} = 3 r^2 X + r^3 \frac{\mathrm{d} X}{\mathrm{d} r}, \end{displaymath}$

where the final equality follows from the result $\frac{\mathrm{d}}{\mathrm{d} y} y^n = ny^{n - 1}$ we obtained in the second part of the post, here, with taken as 3 and taken as . Thus after multiplying the previous equation by , it can be written:

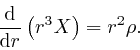
$\begin{displaymath}\frac{\mathrm{d}}{\mathrm{d} r} \left( r^3 X \right) = r^2 \rho . \end{displaymath}$

So from the result we found in the first part of the post, here, that the integral of the rate of change of a quantity is equal to the net change of that quantity, we find that for any two particular values and of :

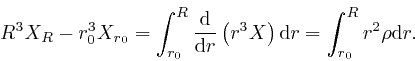
$\begin{displaymath}R^3 X_R - r^3_0 X_{r_0} = \int_{r_0}^R \frac{\mathrm{d}}{\mat... ...3 X \right) \mathrm{d} r = \int_{r_0}^R r^2 \rho \mathrm{d} r. \end{displaymath}$

The expression 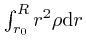$\int_{r_0}^R r^2 \rho \mathrm{d} r$ is the total electric charge in the region between distances and from the centre of the sphere, divided by the surface area of a sphere of radius 1, which I'll represent by . For the surface area of a sphere of radius is , since if we use angular coordinates such as latitude and longitude to specify position on the surface of the sphere, the distance moved as a result of a change of an angular coordinate is proportional to . 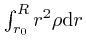Thus the contribution to the integral $\int_{r_0}^R r^2 \rho \mathrm{d} r$ from the interval from to $r + \mathrm{d} r$ is aproximately $\frac{1}{S}$ times the total electric charge in the spherical shell between distances and $r + \mathrm{d} r$ from $\left( 0, 0, 0 \right)$ , since the volume of this shell is approximately $Sr^2 \mathrm{d} r$ , and the errors of these two approximations tend to 0 more rapidly than in proportion to $\mathrm{d} r$ as $\mathrm{d} r$ tends to 0.

Let's now assume that $\rho$ is finite throughout the sphere, and depends smoothly on as tends to 0. Then $X_{r_0}$ is finite as tends to 0, so:

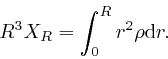
$\begin{displaymath}R^3 X_R = \int_0^R r^2 \rho \mathrm{d} r. \end{displaymath}$

Thus for greater than the radius of the charged sphere, we have:

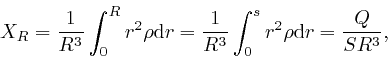
$\begin{displaymath}X_R = \frac{1}{R^3} \int_0^R r^2 \rho \mathrm{d} r = \frac{1}{R^3} \int_0^s r^2 \rho \mathrm{d} r = \frac{Q}{SR^3}, \end{displaymath}$

where is the total electric charge of the sphere. Thus if is outside the sphere, then the electric displacement at is given by:

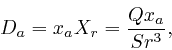
$\begin{displaymath}D_a = x_a X_r = \frac{Qx_a}{Sr^3}, \end{displaymath}$

for . Thus the electric field strength in the region outside the sphere is given by:

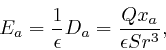
$\begin{displaymath}E_a = \frac{1}{\epsilon} D_a = \frac{Qx_a}{\epsilon Sr^3}, \end{displaymath}$

where $\epsilon$ is the permittivity of the material in the region outside the sphere. So the force on a particle of electric charge at position outside the sphere is given by:

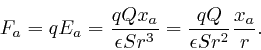
$\begin{displaymath}F_a = qE_a = \frac{qQx_a}{\epsilon Sr^3} = \frac{qQ}{\epsilon Sr^2} \frac{x_a}{r} . \end{displaymath}$

This is in agreement with Coulomb's law, since $\frac{x_a}{r}$ is a vector of length 1, that points along the line from the centre of the sphere to . The force is repulsive if and have the same sign, and attractive if they have opposite signs.

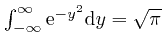We'll calculate the surface area of a sphere of radius 1 by using the result we found in the second part of the post, here, that $\int_{- \infty}^{\infty} \mathrm{e}^{- y^2} \mathrm{d} y = \sqrt{\pi}$ . We have:

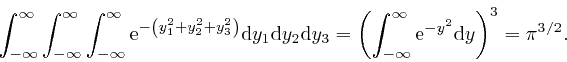
$\begin{displaymath}\int_{- \infty}^{\infty} \int_{- \infty}^{\infty} \int_{- \in... ...ty} \mathrm{e}^{- y^2} \mathrm{d} y \right)^3 = \pi^{3 / 2} . \end{displaymath}$

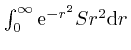We can also think of , , and as the Cartesian coordinates of a point in 3-dimensional Euclidean space. The distance from the point $\left( 0, 0, 0 \right)$ to the point $\left( y_1, y_2, y_3 \right)$ is then $r = \sqrt{y^2_1 + y^2_2 + y^2_3}$ . So from the discussion above, with $\rho$ taken as $\mathrm{e}^{- r^2}$ , the above triple integral is equal to $\int_0^{\infty} \mathrm{e}^{- r^2} Sr^2 \mathrm{d} r$ , so we have:

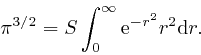
$\begin{displaymath}\pi^{3 / 2} = S \int_0^{\infty} \mathrm{e}^{- r^2} r^2 \mathrm{d} r. \end{displaymath}$

The value of the expression $\mathrm{e}^{- r^2} r^2$ is unaltered if we replace by , so we also have:

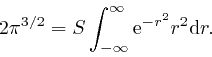
$\begin{displaymath}2 \pi^{3 / 2} = S \int_{- \infty}^{\infty} \mathrm{e}^{- r^2} r^2 \mathrm{d} r. \end{displaymath}$

So from the result we found in the second part of the post, here:

$\begin{displaymath}S = 4 \pi . \end{displaymath}$

Thus the force on a particle of electric charge at position outside the sphere is given by:

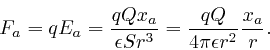
$\begin{displaymath}F_a = qE_a = \frac{qQx_a}{\epsilon Sr^3} = \frac{qQ}{4 \pi \epsilon r^2} \frac{x_a}{r} . \end{displaymath}$

The permittivity of the vacuum is denoted by $\epsilon_0$ . The expression $\frac{1}{4 \pi \epsilon_0}$ is the number that determines the overall strength of the electrostatic force between two stationary charges, so it plays the same role for the electrostatic force as Newton's constant plays for the gravitational force.

The value of the permittivity, $\epsilon$ , whose unit is joule metres per coulomb, or equivalently kilogram metre per second per coulomb, can be measured for a particular electrical insulator by placing a sample of the insulator between the plates of a parallel plate capacitor, which consists of two large parallel conducting plates separated by a thin layer of insulator, then connecting a known voltage source across the plates of the capacitor, and measuring the time integral of the resulting current that flows along the wires from the voltage source to the capacitor, until the current stops flowing. The current is $\pm$ the rate of change of the charge on a plate of the capacitor, so since the integral of the rate of change is the net change, as we found in the first part of the post, here, the time integral of the current is $\pm$ the total electric charge that ends up on a plate of the capacitor.

Once the current has stopped flowing, the voltage no longer changes along the wires from the terminals of the voltage source to the plates of the capacitor, so the entire voltage of the voltage source ends up between the plates of the capacitor. If the lengths of the sides of the capacitor plates are much larger than the distance between the plates, and the 1 and 2 coordinate directions are in the plane of the plates, then the electric field strength between the plates is $E_3 = \frac{V}{l}$ , where is the voltage of the voltage source, and is the distance between the plates.

If the electric charge on a plate of the capacitor is $\pm Q$ and is uniformly distributed over the capacitor plate, and the area of each capacitor plate is , then by integrating Maxwell's equation $\frac{\partial}{\partial x_3} D_3 = \rho$ across the thickness of a capacitor plate and noting that the electric field is 0 outside the plates, we find:

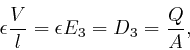
$\begin{displaymath}\epsilon \frac{V}{l} = \epsilon E_3 = D_3 = \frac{Q}{A}, \end{displaymath}$

since the integral of $\frac{\partial}{\partial x_3} D_3$ across the thickness of a capacitor plate is equal to the difference of between the inner and outer faces of that capacitor plate, by the result we found in the first part of the post, here, that the integral of the rate of change of a quantity is equal to the net change of that quantity; and the integral of the electric charge per unit volume, $\rho$ , across the thickness of a capacitor plate is equal to the electric charge per unit area, $\frac{Q}{A}$ , on the capacitor plate.

Thus since , , , and are all known, the value of $\epsilon$ for the electrical insulator between the capacitor plates is determined. From measurements of this type with a vacuum between the capacitor plates, the permittivity $\epsilon_0$ of a vacuum is found to be such that:

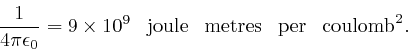
$\begin{displaymath}\frac{1}{4 \pi \epsilon_0} = 9 \times 10^9 \hspace{0.8em} \m... ...em} \mathrm{{{per}}} \hspace{0.8em} \mathrm{{{coulomb}}}^2 . \end{displaymath}$

Maxwell summarized Ampère's law for the force between two parallel electric currents, as above, by the equation:

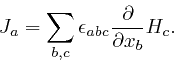
$\begin{displaymath}J_a = \sum_{b, c} \epsilon_{a b c} \frac{\partial}{\partial x_b} H_c . \end{displaymath}$

Here is a vector field called the electric current density. For each position , time , and value 1, 2, or 3 of the coordinate index , it is defined to be the net amount of electric charge that passes in the positive direction through a small area $\mathrm{d} A$ perpendicular to the direction in a small time $\mathrm{d} t$ , divided by $\mathrm{d} A \mathrm{d} t$ , where the ratio is taken in the limit that $\mathrm{d} A$ and $\mathrm{d} t$ tend to 0. The units of are amps per metre. $\epsilon_{a b c}$ is the totally antisymmetric tensor I defined above. is a vector field called the magnetic field strengh, whose relation to the magnetic induction at a position depends on the material present at . The units of are amps per metre. $\frac{\partial}{\partial x_a}$ has the same meaning as in the first part of the post, here, with now taken as , and now taken as .

In most non-magnetized materials the magnetic induction and the magnetic field strength are related by:

$\begin{displaymath}B = \mu H, \end{displaymath}$

where $\mu$ , which is the Greek letter mu, is a number called the permeability of the material. Its unit is kilogram metres per coulomb. The permeability of the vacuum is denoted by $\mu_0$ . Its value is fixed by the definition of the amp, as above.

To check that the above equation summarizing Ampère's law leads to a force between two long straight parallel wires carrying electric currents, whose strength is inversely proportional to the distance between the wires as measured by Ampère, and to calculate the value of $\mu_0$ implied by the definition of the amp, as above, we'll calculate the magnetic field produced by an infinitely long straight wire that is carrying an electric current. We'll choose the wire to be along the 3 direction, and the zero of the 1 and 2 Cartesian coordinates to be at the centre of the wire, and represent the radius of the wire by . We'll assume that $J_{3 x}$ , the electric current density in the direction along the wire at position , does not depend on or the direction from to the centre of the wire, although it might depend on the distance $r = \sqrt{x^2_1 + x^2_2}$ from to the centre of the wire.

From its definition above, the antisymmetric tensor $\epsilon_{a b c}$ is 0 if any two of its indexes are equal, so in particular, $\epsilon_{3 b 3}$ is 0 for all values of the index . Thus Maxwell's equation summarizing Ampère's law, as above, does not relate to , so we'll assume is 0.

Now let's suppose that the magnetic field strength at position is directed along the straight line perpendicular to the wire from to the centre of the wire, so for , where is a quantity that depends on . Then in the same way as above, we find:

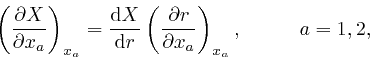
$\begin{displaymath}\left( \frac{\partial X}{\partial x_a} \right)_{x_a} = \frac{... ...artial r}{\partial x_a} \right)_{x_a}, \hspace{1cm} a = 1, 2, \end{displaymath}$

and also in the same way as above, we find:

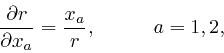
$\begin{displaymath}\frac{\partial r}{\partial x_a} = \frac{x_a}{r}, \hspace{1cm} a = 1, 2, \end{displaymath}$

so:

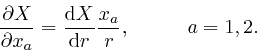
$\begin{displaymath}\frac{\partial X}{\partial x_a} = \frac{\mathrm{d} X}{\mathrm{d} r} \frac{x_a}{r}, \hspace{1cm} a = 1, 2. \end{displaymath}$

From Leibniz's rule for the rate of change of a product, which we obtained in the first part of the post, here, we have:

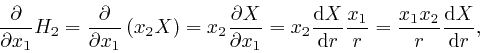
$\begin{displaymath}\frac{\partial}{\partial x_1} H_2 = \frac{\partial}{\partial ... ..._1}{r} = \frac{x_1 x_2}{r} \frac{\mathrm{d} X}{\mathrm{d} r}, \end{displaymath}$

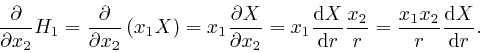
$\begin{displaymath}\frac{\partial}{\partial x_2} H_1 = \frac{\partial}{\partial ... ...2}{r} = \frac{x_1 x_2}{r} \frac{\mathrm{d} X}{\mathrm{d} r} . \end{displaymath}$

Thus:

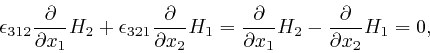
$\begin{displaymath}\epsilon_{312} \frac{\partial}{\partial x_1} H_2 + \epsilon_{... ...l}{\partial x_1} H_2 - \frac{\partial}{\partial x_2} H_1 = 0, \end{displaymath}$

so Maxwell's equation summarizing Ampère's law, as above, does not relate to this form of , so we'll also assume that this form of is 0.

The final possibility is that the magnetic field strength at position is perpendicular to the plane defined by and the wire carrying the current. Then , and from the diagram in the first part of the post, here, interpreted as the two-dimensional plane through and perpendicular to the wire, if $x_1 = r \mathrm{\cos} \left( \theta \right)$ and $x_2 = r \mathrm{\sin} \left( \theta \right)$ , then the direction of is along $\left( - r \mathrm{\sin} \left( \theta \right), r \mathrm{\cos} \left( \theta \right) \right) = \left( - x_2, x_1 \right)$ , so , , where is a quantity that depends on . Then from Leibniz's rule for the rate of change of a product, which we obtained in the first part of the post, here, and the formula above for $\frac{\partial X}{\partial x_a}$ , we have:

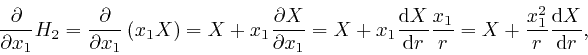
$\begin{displaymath}\frac{\partial}{\partial x_1} H_2 = \frac{\partial}{\partial ... ...{r} = X + \frac{x^2_1}{r} \frac{\mathrm{d} X}{\mathrm{d} r}, \end{displaymath}$

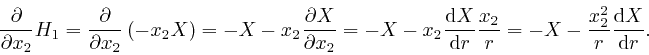
$\begin{displaymath}\frac{\partial}{\partial x_2} H_1 = \frac{\partial}{\partial ... ... = - X - \frac{x^2_2}{r} \frac{\mathrm{d} X}{\mathrm{d} r} . \end{displaymath}$

Thus from Maxwell's equation summarizing Ampère's law, as above:

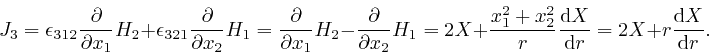
$\begin{displaymath}J_3 = \epsilon_{312} \frac{\partial}{\partial x_1} H_2 + \eps... ...}{\mathrm{d} r} = 2 X + r \frac{\mathrm{d} X}{\mathrm{d} r} . \end{displaymath}$

From Leibniz's rule for the rate of change of a product, we have:

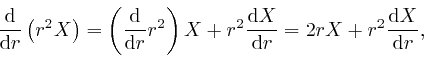
$\begin{displaymath}\frac{\mathrm{d}}{\mathrm{d} r} \left( r^2 X \right) = \left(... ...{\mathrm{d} r} = 2 rX + r^2 \frac{\mathrm{d} X}{\mathrm{d} r}, \end{displaymath}$

where the final equality follows from the result $\frac{\mathrm{d}}{\mathrm{d} y} y^n = ny^{n - 1}$ we obtained in the second part of the post, here, with taken as 2 and taken as . Thus after multiplying the previous equation by , it can be written:

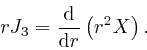
$\begin{displaymath}rJ_3 = \frac{\mathrm{d}}{\mathrm{d} r} \left( r^2 X \right) . \end{displaymath}$

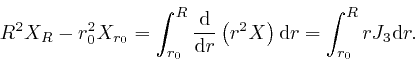
$\begin{displaymath}R^2 X_R - r^2_0 X_{r_0} = \int_{r_0}^R \frac{\mathrm{d}}{\mat... ...( r^2 X \right) \mathrm{d} r = \int_{r_0}^R rJ_3 \mathrm{d} r. \end{displaymath}$

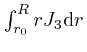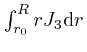The expression $\int_{r_0}^R rJ_3 \mathrm{d} r$ is $\frac{1}{2 \pi}$ times the total electric charge per unit time passing through the region between distances and from the centre of the wire, in any cross-section of the wire. For the circumference of a circle of radius is $2 \pi r$ , so the contribution to the integral $\int_{r_0}^R rJ_3 \mathrm{d} r$ from the interval from to $r + \mathrm{d} r$ is aproximately $\frac{1}{2 \pi}$ times the total electric charge per unit time passing through the region between distances and $r + \mathrm{d} r$ from the centre of the wire, in any cross-section of the wire, since the area of this shell is approximately $2 \pi r \mathrm{d} r$ , and the errors of these two approximations tend to 0 more rapidly than in proportion to $\mathrm{d} r$ as $\mathrm{d} r$ tends to 0.

Let's now assume that is finite throughout the cross-section of the wire, and depends smoothly on as tends to 0. Then $X_{r_0}$ is finite as tends to 0, so:

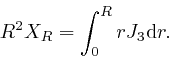
$\begin{displaymath}R^2 X_R = \int_0^R rJ_3 \mathrm{d} r. \end{displaymath}$

Thus for greater than the radius of the wire, we have:

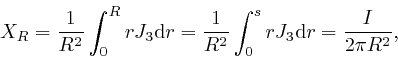
$\begin{displaymath}X_R = \frac{1}{R^2} \int_0^R rJ_3 \mathrm{d} r = \frac{1}{R^2} \int_0^s rJ_3 \mathrm{d} r = \frac{I}{2 \pi R^2}, \end{displaymath}$

where is the total electric current carried by the wire. Thus if is outside the wire, then the magnetic field strength at is given by:

$\begin{displaymath}H_1 = - x_2 X_r = - \frac{Ix_2}{2 \pi r^2}, \hspace{2cm} H_2 = x_1 X_r = \frac{Ix_1}{2 \pi r^2} . \end{displaymath}$

Thus the magnetic induction in the region outside the wire is given by:

$\begin{displaymath}\left( B_1, B_2, B_3 \right) = \mu \left( H_1, H_2, H_3 \righ... ... I}{2 \pi r} \left( - \frac{x_2}{r}, \frac{x_1}{r}, 0 \right), \end{displaymath}$

where $\mu$ is the permeability of the material in the region outside the wire. This is perpendicular to the plane defined by the point and the wire, and its magnitude is proportional to the current in the wire, and inversely proportional to the distance of the point from the wire, in agreement with the measurements of Biot and Savart as above, since $\left( - \frac{x_2}{r}, \frac{x_1}{r}, 0 \right)$ is a vector of length 1.

Let's now suppose there is a second infinitely long straight wire parallel to the first, such that the 1 and 2 Cartesian coordinates of the centre of the second wire are $\left( x_1, x_2 \right)$ , and the total electric current carried by the second wire is $I_{\mathrm{2{{nd}}}}$ . From Maxwell's equation above, and the definition of the antisymmetric tensor $\epsilon_{a b c}$ as above, the force on a particle of electric charge moving with velocity $v = \left( 0, 0, v_3 \right)$ along the second wire, in the presence of the magnetic field produced by the first wire, as above, is given by:

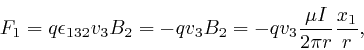
$\begin{displaymath}F_1 = q \epsilon_{1 3 2} v_3 B_2 = - qv_3 B_2 = - qv_3 \frac{\mu I}{2 \pi r} \frac{x_1}{r}, \end{displaymath}$

$\begin{displaymath}F_2 = q \epsilon_{2 3 1} v_3 B_1 = qv_3 B_1 = - qv_3 \frac{\mu I}{2 \pi r} \frac{x_2}{r}, \end{displaymath}$

$\begin{displaymath}F_3 = 0. \end{displaymath}$

The interaction between this moving charge and the other particles in the second wire prevents this moving charge from accelerating sideways out of the second wire, so the above force is a contribution to the force on the second wire, that results from the magnetic field produced by the current in the first wire. If there are particles of electric charge and velocity $\left( 0, 0, v_3 \right)$ per unit length of the second wire, then their contribution to the force per unit length on the second wire is:

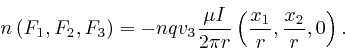
$\begin{displaymath}n \left( F_1, F_2, F_3 \right) = - nqv_3 \frac{\mu I}{2 \pi r} \left( \frac{x_1}{r}, \frac{x_2}{r}, 0 \right) . \end{displaymath}$

The average number of these particles that pass through any cross-section of the second wire per unit time is , so their contribution to the electric current carried by the second wire is . Thus the contribution of these particles to the force per unit length on the second wire is $- \frac{\mu I}{2 \pi r} \left( \frac{x_1}{r}, \frac{x_2}{r}, 0 \right)$ times their contribution to the electric current carried by the second wire. So by adding up the contributions from charged particles of all relevant values of and , we find that the total force per unit length on the second wire that results from the current carried by the first wire and the current $I_{\mathrm{2{{nd}}}}$ carried by the second wire is given by:

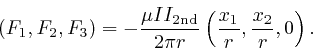
$\begin{displaymath}\left( F_1, F_2, F_3 \right) = - \frac{\mu II_{\mathrm{2{{nd}}}}}{2 \pi r} \left( \frac{x_1}{r}, \frac{x_2}{r}, 0 \right) . \end{displaymath}$

The direction of this force is towards the first wire if and $I_{\mathrm{2{{nd}}}}$ have the same sign and away from the first wire if and $I_{\mathrm{2{{nd}}}}$ have opposite sign, and the strength of this force is proportional to the product of the currents, and inversely proportional to the distance between the wires, so this force is in agreement with Ampère's law, as above. And from the definition of the amp, as above, we find that the permeability $\mu_0$ of a vacuum is by definition given by:

$\begin{displaymath}\mu_0 = 4 \pi \times 10^{- 7} \hspace{0.8em} \mathrm{{{kilog... ...em} \mathrm{{{per}}} \hspace{0.8em} \mathrm{{{coulomb}}}^2 . \end{displaymath}$

Maxwell noticed that his equation summarizing Ampère's law, as above, leads to a contradiction. For by applying $\frac{\partial}{\partial x_a}$ to both sides of that equation, and summing over , we obtain:

$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} J_a = \sum_{a, b, c} \ep... ...ac{\partial}{\partial x_a} \frac{\partial}{\partial x_b} H_c . \end{displaymath}$

For a quantity that depends smoothly on a number of quantities that can vary continuously, where represents the collection of those quantities, and indexes such as or distinguish the quantities in the collection, we have:

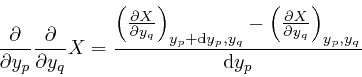
$\begin{displaymath}\frac{\partial}{\partial y_p} \frac{\partial}{\partial y_q} X... ...\partial X}{\partial y_q} \right)_{y_p, y_q}}{\mathrm{d} y_p} \end{displaymath}$

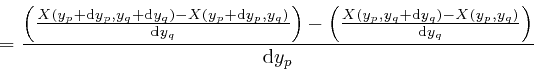
$\begin{displaymath}= \frac{\left( \frac{X \left( y_p + \mathrm{d} y_p, y_q + \ma... ...ft( y_p, y_q \right)}{\mathrm{d} y_q} \right)}{\mathrm{d} y_p} \end{displaymath}$

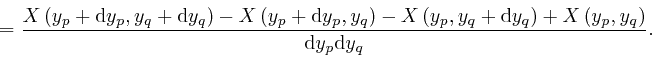
$\begin{displaymath}= \frac{X \left( y_p + \mathrm{d} y_p, y_q + \mathrm{d} y_q \... ... + X \left( y_p, y_q \right)}{\mathrm{d} y_p \mathrm{d} y_q} . \end{displaymath}$

The expression in the third line here is equal to the expression we obtain from it by swapping the indexes and , so we have:

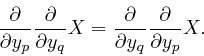
$\begin{displaymath}\frac{\partial}{\partial y_p} \frac{\partial}{\partial y_q} X... ...\frac{\partial}{\partial y_q} \frac{\partial}{\partial y_p} X. \end{displaymath}$

So if the magnetic field strength depends smoothly on position, we also have:

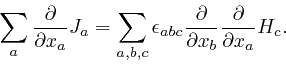
$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} J_a = \sum_{a, b, c} \ep... ...ac{\partial}{\partial x_b} \frac{\partial}{\partial x_a} H_c . \end{displaymath}$

The value of the right-hand side of this formula does not depend on the particular letters , , and used for the indexes that are summed over. Thus if the letter , used as an index, is also understood to have the possible values 1, 2, or 3, we have:

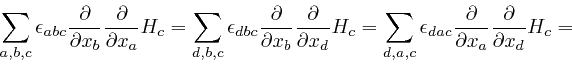
$\begin{displaymath}\sum_{a, b, c} \epsilon_{a b c} \frac{\partial}{\partial x_b}... ...{\partial}{\partial x_a} \frac{\partial}{\partial x_d} H_c = \end{displaymath}$

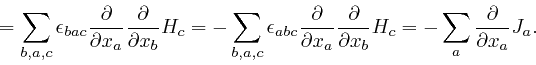
$\begin{displaymath}= \sum_{b, a, c} \epsilon_{b a c} \frac{\partial}{\partial x_... ...rtial x_b} H_c = - \sum_a \frac{\partial}{\partial x_a} J_a . \end{displaymath}$

At each of the first three steps in the above formula, one of the indexes summed over in the previous version of the expression is rewritten as a different letter that is understood to take the same possible values, 1, 2, or 3, and which does not otherwise occur in the expression. At the first step, the index is rewritten as , then at the second step, the index is rewritten as , and at the third step, the index is rewritten as . An index that occurs in an expression, but is summed over the range of its possible values, so that the full expression, including the $\sum$ , does not depend on the value of that index, is called a "dummy index".

The fourth step in the above formula used the definition of the antisymmetric tensor $\epsilon_{a b c}$ , as above, which implies that its value is multiplied by if two of its indexes are swapped, so that $\epsilon_{b a c} = - \epsilon_{a b c}$ . The fifth step used the original formula for $\sum_a \frac{\partial}{\partial x_a} J_a$ , as above, together with the fact that the order of the indexes under the $\sum$ in the right-hand side doesn't matter, since each of the indexes is simply summed over the values 1, 2, and 3.

Thus from the second formula for $\sum_a \frac{\partial}{\partial x_a} J_a$ , as above, we have:

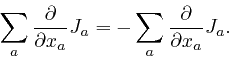
$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} J_a = - \sum_a \frac{\partial}{\partial x_a} J_a . \end{displaymath}$

Hence:

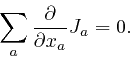
$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} J_a = 0. \end{displaymath}$

Let's now consider the rate of change with time of the total electric charge in a tiny box-shaped region centred at a position , such that the edges of the box are aligned with the coordinate directions, and have lengths $\varepsilon_1$ , $\varepsilon_2$ , and $\varepsilon_3$ . From the definition above of the electric current density , the net amount of electric charge that flows into the box through the face of the box perpendicular to the 1 direction and centred at $\left( x_1 - \frac{1}{2} \varepsilon_1, x_2, x_3 \right)$ , during a small time $\mathrm{d} t$ , is approximately $J_1 \left( x_1 - \frac{1}{2} \varepsilon_1, x_2, x_3 \right) \varepsilon_2 \varepsilon_3 \mathrm{d} t$ , and the net amount of electric charge that flows out of the box through the face of the box perpendicular to the 1 direction and centred at $\left( x_1 + \frac{1}{2} \varepsilon_1, x_2, x_3 \right)$ , during the same small time $\mathrm{d} t$ , is approximately $J_1 \left( x_1 + \frac{1}{2} \varepsilon_1, x_2, x_3 \right) \varepsilon_2 \varepsilon_3 \mathrm{d} t$ , and the errors of these approximations tend to 0 more rapidly than in proportion to $\varepsilon_2 \varepsilon_3 \mathrm{d} t$ , as $\varepsilon_2$ , $\varepsilon_3$ , and $\mathrm{d} t$ tend to 0. And from the result we obtained in the first part of the post, here, with $y_{\left( 0 \right)}$ taken as and taken as $x \pm \frac{1}{2} \left( \varepsilon_1, 0, 0 \right)$ , we have:

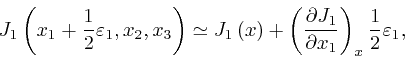
$\begin{displaymath}J_1 \left( x_1 + \frac{1}{2} \varepsilon_1, x_2, x_3 \right) ... ...rtial J_1}{\partial x_1} \right)_x \frac{1}{2} \varepsilon_1, \end{displaymath}$

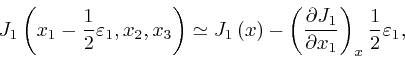
$\begin{displaymath}J_1 \left( x_1 - \frac{1}{2} \varepsilon_1, x_2, x_3 \right) ... ...rtial J_1}{\partial x_1} \right)_x \frac{1}{2} \varepsilon_1, \end{displaymath}$

where the error of the above approximations tends to 0 more rapidly than in proportion to $\varepsilon_1$ , as $\varepsilon_1$ tends to 0. Thus the net amount of electric charge that flows into the box through the faces of the box perpendicular to the 1 direction, during a small time $\mathrm{d} t$ , is approximately:

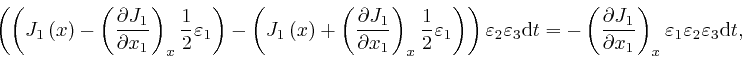
$\begin{displaymath}\left( \left( J_1 \left( x \right) - \left( \frac{\partial J_... ...ht)_x \varepsilon_1 \varepsilon_2 \varepsilon_3 \mathrm{d} t, \end{displaymath}$

where the error of this approximation tends to 0 more rapidly than in proportion to $\varepsilon_1 \varepsilon_2 \varepsilon_3 \mathrm{d} t$ , as $\varepsilon_1$ , $\varepsilon_2$ , $\varepsilon_3$ , and $\mathrm{d} t$ tend to 0. So from the corresponding results for the net amount of electric charge that flows into the box through the faces of the box perpendicular to the 2 and 3 directions, during the same small time $\mathrm{d} t$ , we find that the net amount of electric charge that flows into the box through all the faces of the box, during the small time $\mathrm{d} t$ , is approximately:

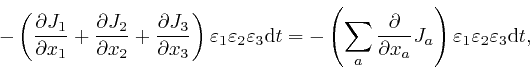
$\begin{displaymath}- \left( \frac{\partial J_1}{\partial x_1} + \frac{\partial J... ...ight) \varepsilon_1 \varepsilon_2 \varepsilon_3 \mathrm{d} t, \end{displaymath}$

There's no evidence that electric charge can vanish into nothing or appear from nothing, so the net amount of electric charge that flows into the box through all the faces of the box, during the small time $\mathrm{d} t$ , must be equal to the net increase of the total electric charge in the box, during the small time $\mathrm{d} t$ , which from the definition of the electric charge density $\rho$ , as above, is approximately:

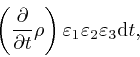
$\begin{displaymath}\left( \frac{\partial}{\partial t} \rho \right) \varepsilon_1 \varepsilon_2 \varepsilon_3 \mathrm{d} t, \end{displaymath}$

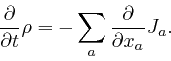
$\begin{displaymath}\frac{\partial}{\partial t} \rho = - \sum_a \frac{\partial}{\partial x_a} J_a . \end{displaymath}$

But we found above that Maxwell's equation summarizing Ampère's law, as above, leads instead to $\sum_a \frac{\partial}{\partial x_a} J_a = 0$ . This equation is false whenever there is a build-up of electric charge in a region, as, for example, on the plates of a parallel plate capacitor, in the method of measuring the permittivity $\epsilon$ of an electrical insulator, that I described above. Maxwell realized that the resolution of this paradox is that there must be an additional term $\frac{\partial}{\partial t} D_a$ in the left-hand side of his equation summarizing Ampère's law, where is the electric displacement vector field, so that the corrected form of his equation summarizing Ampère's law is:

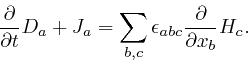
$\begin{displaymath}\frac{\partial}{\partial t} D_a + J_a = \sum_{b, c} \epsilon_{a b c} \frac{\partial}{\partial x_b} H_c . \end{displaymath}$

This equation still correctly reproduces Ampère's law and the magnetic field produced by an electric current flowing in a long straight wire as measured by Biot and Savart, as I described above, because the experiments of Ampère and Biot and Savart were carried out in steady state conditions, where nothing changed with time, so the new term in the left-hand side gave 0. However if we apply $\frac{\partial}{\partial x_a}$ to both sides of this corrected equation, and sum over , which is what led to the paradox for the original equation, we now find:

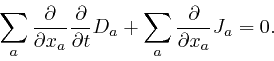
$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} \frac{\partial}{\partial t} D_a + \sum_a \frac{\partial}{\partial x_a} J_a = 0. \end{displaymath}$

So if the electric displacement depends smoothly on position, so that $\frac{\partial}{\partial x_a} \frac{\partial}{\partial t} D_a = \frac{\partial}{\partial t} \frac{\partial}{\partial x_a} D_a$ , by the result we found above, we find:

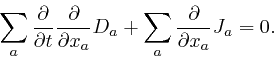
$\begin{displaymath}\sum_a \frac{\partial}{\partial t} \frac{\partial}{\partial x_a} D_a + \sum_a \frac{\partial}{\partial x_a} J_a = 0. \end{displaymath}$

Combining this with Maxwell's equations summarizing Coulomb's law, as above, it gives:

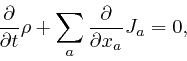
$\begin{displaymath}\frac{\partial}{\partial t} \rho + \sum_a \frac{\partial}{\partial x_a} J_a = 0, \end{displaymath}$

which is now in agreement with the formula expressing the conservation of electric charge, as above.

Michael Faraday discovered in 1831 that if an electrically insulated wire is arranged so that somewhere along its length it forms a loop, and the magnetic induction field inside the loop and perpendicular to the plane of the loop is changed, for example by switching on a current in a separate coil of wire in a suitable position near the loop, then a voltage is temporarily generated along the wire while the magnetic induction field is changing, such that if the directions of the 1 and 2 Cartesian coordinates are in the plane of the loop, and the value of in the region enclosed by the loop in the plane of the loop depends on time but not on position within that region, then:

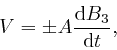
$\begin{displaymath}V = \pm A \frac{\mathrm{d} B_3}{\mathrm{d} t}, \end{displaymath}$

where is the area enclosed by the loop, and the sign depends on the direction along the wire in which the voltage is measured. The sign of the voltage is such that if a current flows along the wire in consequence of the voltage, then the magnetic field $B_{\mathrm{{{prd}}}}$ produced by that current, as above, is such that $\left( B_{\mathrm{{{prd}}}} \right)_3$ in the region enclosed by the loop in the plane of the loop has the opposite sign to $\frac{\mathrm{d} B_3}{\mathrm{d} t}$ .

Maxwell assumed that the electric field strength that corresponds to the voltage is produced by the changing magnetic induction field even when there is no wire present to detect in a convenient way. To discover the consequences of this assumption, it is helpful to know about the relation between the electric field strength and the rate of change of voltage with distance in a particular direction.

For any vector , and any vector of length 1, the expression $\sum_a n_a X_a$ is called the component of in the direction . To relate this to the magnitude $\left\vert X \right\vert$ of , which is $\sqrt{\sum_a X_a X_a}$ by Pythagoras, and the angle $\theta$ between the directions of and , we observe that $\frac{X}{\left\vert X \right\vert}$ is a vector of length 1, and if we consider and $\frac{X}{\left\vert X \right\vert}$ as representing the Cartesian coordinates of two points in the 3-dimensional generalization of Euclidean geometry, as in the first part of this post, here, then by Pythagoras, the distance between those points is:

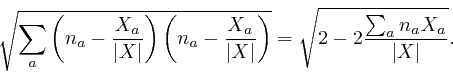
$\begin{displaymath}\sqrt{\sum_a \left( n_a - \frac{X_a}{\left\vert X \right\vert... ...sqrt{2 - 2 \frac{\sum_a n_a X_a}{\left\vert X \right\vert}} . \end{displaymath}$

If does not point either in the same direction as or the opposite direction to , so that is not equal to $\pm \frac{X}{\left\vert X \right\vert}$ , then the directions of and define a 2-dimensional plane, and we can choose Cartesian coordinates in that 2-dimensional plane as in the first part of the post, here, such that the coordinates of are $\left( 1, 0 \right)$ , and the coordinates of $\frac{X}{\left\vert X \right\vert}$ are $\left( \mathrm{\cos} \left( \theta \right), \mathrm{\sin} \left( \theta \right) \right)$ . So by Pythagoras, the distance between the points they define is:

$\begin{displaymath}\sqrt{\left( 1 - \mathrm{\cos} \left( \theta \right) \right)^... ...t)^2} = \sqrt{2 - 2 \: \mathrm{\cos} \left( \theta \right)} . \end{displaymath}$

This is equal to the previous expression, so we have:

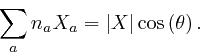
$\begin{displaymath}\sum_a n_a X_a = \left\vert X \right\vert \mathrm{\cos} \left( \theta \right) . \end{displaymath}$

This formula is also true when $n = \pm \frac{X}{\left\vert X \right\vert}$ , so $\mathrm{\cos} \left( \theta \right) = \pm 1$ . If is along the coordinate direction, this formula shows that $X_a = \left\vert X \right\vert \mathrm{\cos} \left( \theta_a \right)$ , where $\theta_a$ is the angle between the direction of and the coordinate direction. Thus for any vector of length 1, $\sum_a n_a X_a$ is equal to the value that the coordinate of in the direction would have, if was one of the coordinate directions of Cartesian coordinates.

If the electric field strength can be derived from a voltage field , so that $E_a = - \frac{\partial V}{\partial x_a}$ as above, then at each point along the electrically insulated wire, we have:

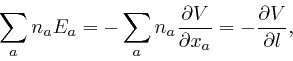
$\begin{displaymath}\sum_a n_a E_a = - \sum_a n_a \frac{\partial V}{\partial x_a} = - \frac{\partial V}{\partial l}, \end{displaymath}$

where is the distance along the wire from that point to a fixed end of the wire, and is a vector of length 1 whose direction is along the wire in the direction of increasing . The first equality here is the component of the equation $E_a = - \frac{\partial V}{\partial x_a}$ in the direction along the wire. The component of $\frac{\partial V}{\partial x_a}$ in any direction is the rate of change of with distance in that direction, so the component of $\frac{\partial V}{\partial x_a}$ in the direction along the wire is the rate of change of with distance along the wire, which is the second equality.

The movable electrically charged particles in the wire are channelled by the electrical insulation of the wire so that their net motion can only be along the wire, and only the component of the electric field strength along the wire can affect their net motion. Their motion along the wire due to the force $\sum_a n_a F_a = q \sum_a n_a E_a$ is determined by a voltage defined along the wire such that

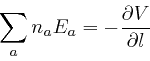
$\begin{displaymath}\sum_a n_a E_a = - \frac{\partial V}{\partial l} \end{displaymath}$

as in the previous formula, even if the voltage defined along the wire does not correspond to a voltage field in the region outside the wire.

Let's consider Faraday's result, as above, for a very small rectangular loop centred at $x_{\left( 0 \right)}$ , such that the edges of the loop are in the 1 and 2 Cartesian coordinate directions and have lengths $\varepsilon_1$ and $\varepsilon_2$ . We'll assume that the wire arrives at and leaves the rectangle at the corner at $\left( x_1, x_2 \right) = \left( x_{\left( 0 \right) 1} - \frac{1}{2} \varepsilon_1, x_{\left( 0 \right) 2} - \frac{1}{2} \varepsilon_2 \right)$ , and that the two lengths of wire that run from this corner of the rectangle to the measuring equipment, such as a voltmeter, follow exactly the same path. Then if the voltage along the wire is related to an electric field strength as in the above formula, the net voltage difference between the ends of the wire, as measured by Faraday, must be produced by the electric field strength along the sides of the rectangle, because any voltages produced along the lengths of wire that run from the corner of the rectangle to the measuring equipment will be equal and opposite along the two lengths of wire, and thus cancel out of the net voltage.

We'll choose to be the distance along the wire from the end of the wire such that increases along the side of the rectangle from the corner at $\left( x_1, x_2 \right) = \left( x_{\left( 0 \right) 1} - \frac{1}{2} \varepsilon_1, x_{\left( 0 \right) 2} - \frac{1}{2} \varepsilon_2 \right)$ to the corner at $\left( x_{\left( 0 \right) 1} + \frac{1}{2} \varepsilon_1, x_{\left( 0 \right) 2} - \frac{1}{2} \varepsilon_2 \right)$ , then along the side from this corner to the corner at $\left( x_{\left( 0 \right) 1} + \frac{1}{2} \varepsilon_1, x_{\left( 0 \right) 2} + \frac{1}{2} \varepsilon_2 \right)$ , then along the side from this corner to the corner at $\left( x_{\left( 0 \right) 1} - \frac{1}{2} \varepsilon_1, x_{\left( 0 \right) 2} + \frac{1}{2} \varepsilon_2 \right)$ , and finally along the side from this corner to the first corner at $\left( x_{\left( 0 \right) 1} - \frac{1}{2} \varepsilon_1, x_{\left( 0 \right) 2} - \frac{1}{2} \varepsilon_2 \right)$ . The components $\left( n_1, n_2 \right)$ of the vector of length 1, that points along the four sides of the rectangle in the direction of increasing , are therefore $\left( 1, 0 \right)$ , $\left( 0, 1 \right)$ , $\left( - 1, 0 \right)$ , and $\left( 0, - 1 \right)$ , for the four sides of the rectangle taken in this order.

The net change of the voltage around the rectangle in the direction of increasing is equal to the sum of the net change of the voltage along the four sides of the rectangle in the direction of increasing , so from the formula above, and the result we found in the first part of the post, here, that the integral of the rate of change of a quantity is equal to the net change of that quantity, is equal to the sum of the integrals $- \int \left( n_1 E_1 + n_2 E_2 \right) \mathrm{d} l$ along the four sides of the rectangle.

For near $x_{\left( 0 \right)}$ in the plane of the rectangle, the result we obtained in the first part of the post, here, with $y_{\left( 0 \right)}$ taken as $x_{\left( 0 \right)}$ and taken as , gives:

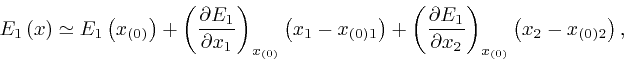
$\begin{displaymath}E_1 \left( x \right) \simeq E_1 \left( x_{\left( 0 \right)} \... ...eft( 0 \right)}} \left( x_2 - x_{\left( 0 \right) 2} \right), \end{displaymath}$

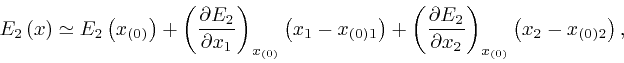
$\begin{displaymath}E_2 \left( x \right) \simeq E_2 \left( x_{\left( 0 \right)} \... ...eft( 0 \right)}} \left( x_2 - x_{\left( 0 \right) 2} \right), \end{displaymath}$

where as the magnitudes of $x_1 - x_{\left( 0 \right) 1}$ and $x_2 - x_{\left( 0 \right) 2}$ tend to 0, the error of this approximate representation tends to 0 more rapidly than in proportion to those magnitudes.

The coordinates $\left( x_1, x_2 \right)$ of a point a distance along the first side of the rectangle from the first corner of this side are $\left( x_1, x_2 \right) = \left( x_{\left( 0 \right) 1} - \frac{1}{2} \varepsilon_1 + s, x_{\left( 0 \right) 2} - \frac{1}{2} \varepsilon_2 \right)$ . And along this side, is equal to plus a constant value, the length of the wire from its first end to the first corner of this side, so $\frac{\mathrm{d} l}{\mathrm{d} s} = 1$ . Thus since $\left( n_1, n_2 \right) = \left( 1, 0 \right)$ for this side, we have:

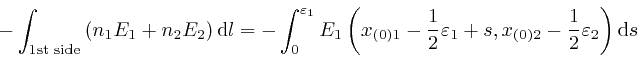
$\begin{displaymath}- \int_{\mathrm{1{{st}}} \; \mathrm{{{side}}}} \left( n_1 E_... ...0 \right) 2} - \frac{1}{2} \varepsilon_2 \right) \mathrm{d} s \end{displaymath}$

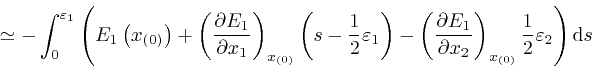
$\begin{displaymath}\simeq - \int_0^{\varepsilon_1} \left( E_1 \left( x_{\left( 0... ...t( 0 \right)}} \frac{1}{2} \varepsilon_2 \right) \mathrm{d} s \end{displaymath}$

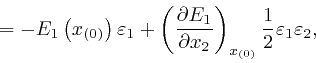
$\begin{displaymath}= - E_1 \left( x_{\left( 0 \right)} \right) \varepsilon_1 + \... ..._{\left( 0 \right)}} \frac{1}{2} \varepsilon_1 \varepsilon_2, \end{displaymath}$

where the error of this approximation tends to 0 more rapidly than in proportion to $\varepsilon^2_1$ or $\varepsilon_1 \varepsilon_2$ as $\varepsilon_1$ and $\varepsilon_2$ tend to 0, and I used the result we found in the first part of the post, here, that the integral of the rate of change of a quantity is equal to the net change of that quantity, and also $\frac{\mathrm{d} s}{\mathrm{d} s} = 1$ and $\frac{\mathrm{d}}{\mathrm{d} s} s^2 = 2 s$ , from the result we found in the second part of the post, here.

The coordinates $\left( x_1, x_2 \right)$ of a point a distance along the third side of the rectangle from the first corner of that side are $\left( x_1, x_2 \right) = \left( x_{\left( 0 \right) 1} + \frac{1}{2} \varepsilon_1 - s, x_{\left( 0 \right) 2} + \frac{1}{2} \varepsilon_2 \right)$ . We again have $\frac{\mathrm{d} l}{\mathrm{d} s} = 1$ , so since $\left( n_1, n_2 \right) = \left( - 1, 0 \right)$ for that side, we have:

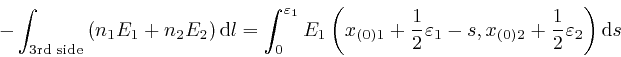
$\begin{displaymath}- \int_{\mathrm{3{{rd}}} \; \mathrm{{{side}}}} \left( n_1 E_... ...0 \right) 2} + \frac{1}{2} \varepsilon_2 \right) \mathrm{d} s \end{displaymath}$

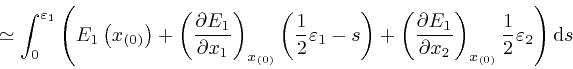
$\begin{displaymath}\simeq \int_0^{\varepsilon_1} \left( E_1 \left( x_{\left( 0 \... ...t( 0 \right)}} \frac{1}{2} \varepsilon_2 \right) \mathrm{d} s \end{displaymath}$

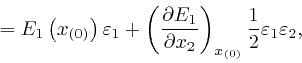
$\begin{displaymath}= E_1 \left( x_{\left( 0 \right)} \right) \varepsilon_1 + \le... ..._{\left( 0 \right)}} \frac{1}{2} \varepsilon_1 \varepsilon_2, \end{displaymath}$

to the same accuracy as before. Thus:

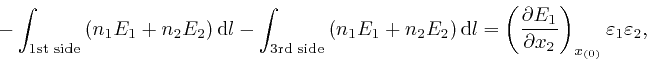
$\begin{displaymath}- \int_{\mathrm{1{{st}}} \; \mathrm{{{side}}}} \left( n_1 E_... ...} \right)_{x_{\left( 0 \right)}} \varepsilon_1 \varepsilon_2, \end{displaymath}$

where the error of this approximation tends to 0 more rapidly than in proportion to $\varepsilon_1 \varepsilon_2$ , as $\varepsilon_1$ and $\varepsilon_2$ tend to 0 with their ratio fixed to a finite non-zero value.

Similarly we find:

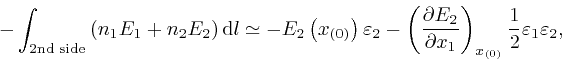
$\begin{displaymath}- \int_{\mathrm{2{{nd}}} \; \mathrm{{{side}}}} \left( n_1 E_... ..._{\left( 0 \right)}} \frac{1}{2} \varepsilon_1 \varepsilon_2, \end{displaymath}$

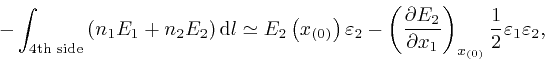
$\begin{displaymath}- \int_{\mathrm{4{{th}}} \; \mathrm{{{side}}}} \left( n_1 E_... ..._{\left( 0 \right)}} \frac{1}{2} \varepsilon_1 \varepsilon_2, \end{displaymath}$

to the same accuracy. So:

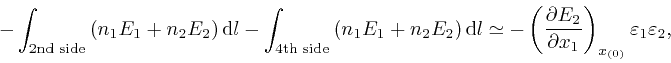
$\begin{displaymath}- \int_{\mathrm{2{{nd}}} \; \mathrm{{{side}}}} \left( n_1 E_... ...} \right)_{x_{\left( 0 \right)}} \varepsilon_1 \varepsilon_2, \end{displaymath}$

to the same accuracy. Thus:

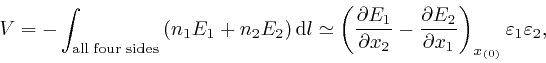
$\begin{displaymath}V = - \int_{\mathrm{{{all}}} \; \mathrm{{{four}}} \; \mathr... ...} \right)_{x_{\left( 0 \right)}} \varepsilon_1 \varepsilon_2, \end{displaymath}$

Thus from Faraday's measurements, as above:

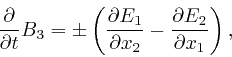
$\begin{displaymath}\frac{\partial}{\partial t} B_3 = \pm \left( \frac{\partial E_1}{\partial x_2} - \frac{\partial E_2}{\partial x_1} \right), \end{displaymath}$

since $\varepsilon_1 \varepsilon_2$ is the area of the small rectangle. We have obtained this equation at the position $x_{\left( 0 \right)}$ of the centre of the small rectangle, so it holds everywhere the small rectangle of wire could have been placed.

To determine the sign, let's suppose that and are 0 at the centre of the small rectangle, and that is positive along the 1st side of the rectangle and negative along the 3rd side, and is positive along the 2nd side of the rectangle and negative along the 4th side. Then $\frac{\partial E_1}{\partial x_2}$ is negative and $\frac{\partial E_2}{\partial x_1}$ is positive, so $\frac{\partial E_1}{\partial x_2} - \frac{\partial E_2}{\partial x_1}$ is negative, and the force $\sum_a n_a F_a = q \sum_a n_a E_a$ on a movable charged particle of positive is in the direction of increasing along all four sides of the rectangle, so the current along the wire is positive in the direction of increasing .

From the result we found above, Maxwell's equation summarizing Ampère's law, as above, implies that a positive current along a wire in the 3 direction produces a magnetic induction field $B_{\mathrm{{{prd}}}}$ such that $\left( B_{\mathrm{{{prd}}}} \right)_1$ is negative for greater than the coordinate of the wire and positive otherwise, and $\left( B_{\mathrm{{{prd}}}} \right)_2$ is positive for greater than the coordinate of the wire and negative otherwise.

The antisymmetric tensor $\epsilon_{a b c}$ , which I defined above, is unaltered by a cyclic permutation of its indexes, for example $1, 2, 3 \rightarrow 3, 1, 2$ or $3, 1, 2 \rightarrow 2, 3, 1$ , so Maxwell's equation summarizing Ampère's law, as above, also implies that a positive current along a wire in the 1 direction produces a magnetic induction field $B_{\mathrm{{{prd}}}}$ such that $\left( B_{\mathrm{{{prd}}}} \right)_3$ is positive for greater than the coordinate of the wire and negative otherwise, and a positive current along a wire in the 2 direction produces a magnetic induction field $B_{\mathrm{{{prd}}}}$ such that $\left( B_{\mathrm{{{prd}}}} \right)_3$ is negative for greater than the coordinate of the wire and positive otherwise.

Thus if the current along the wire is positive in the direction of increasing , the magnetic induction field $B_{\mathrm{{{prd}}}}$ produced by the current along each side of the small rectangle is such that $\left( B_{\mathrm{{{prd}}}} \right)_3$ is positive inside the small rectangle. So from the observed sign of the voltage, as I described above, a positive value of $\frac{\mathrm{d} B_3}{\mathrm{d} t}$ inside the small rectangle produces electric field strengths that result in a current along the wire that is negative in the direction of increasing , and thus of opposite sign to those I assumed above. Thus positive $\frac{\mathrm{d} B_3}{\mathrm{d} t}$ produces positive $\frac{\partial E_1}{\partial x_2} - \frac{\partial E_2}{\partial x_1}$ , so the formula with the correct sign is:

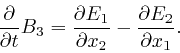
$\begin{displaymath}\frac{\partial}{\partial t} B_3 = \frac{\partial E_1}{\partial x_2} - \frac{\partial E_2}{\partial x_1} . \end{displaymath}$

The corresponding formulae that result from considering small rectangles whose edges are in the 2 and 3 or 3 and 1 Cartesian coordinate directions are obtained from this formula by cyclic permutation of the indexes, and the three formulae can be written as:

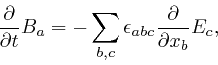
$\begin{displaymath}\frac{\partial}{\partial t} B_a = - \sum_{b, c} \epsilon_{a b c} \frac{\partial}{\partial x_b} E_c, \end{displaymath}$

where $\epsilon_{a b c}$ is the totally antisymmetric tensor I defined above. This is Maxwell's equation summarizing Faraday's measurements involving time-dependent magnetic fields, as above.

From the discussion above, if the electric field strength can be derived from a voltage field , then $E_a = - \frac{\partial V}{\partial x_a}$ . The electric field strength produced by the changing magnetic induction field in accordance with the above equation cannot be derived from a voltage field , for if $E_a = - \frac{\partial V}{\partial x_a}$ , and depends smoothly on position, then by a similar calculation to the one above, we have:

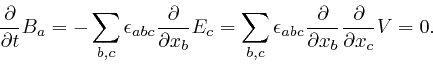
$\begin{displaymath}\frac{\partial}{\partial t} B_a = - \sum_{b, c} \epsilon_{a b... ...c{\partial}{\partial x_b} \frac{\partial}{\partial x_c} V = 0. \end{displaymath}$

No magnetically charged particles, often referred to as magnetic monopoles, have yet been observed, and Maxwell's equation summarizing this fact, analogous to his equation summarizing Coulomb's law, as above, is:

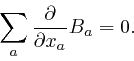
$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} B_a = 0. \end{displaymath}$

Although it's not possible to derive the electric field strength from a voltage field alone if the magnetic induction field is time-dependent, Maxwell's equation summarizing Faraday's measurements involving time-dependent magnetic fields, as above, and his equation above summarizing the non-observation of magnetic monopoles, can always be solved by deriving the electric field strength and the magnetic induction field from a voltage field and a vector field called the vector potential, such that:

$\begin{displaymath}E_a = - \frac{\partial V}{\partial x_a} - \frac{\partial A_a}{\partial t}, \end{displaymath}$

$\begin{displaymath}B_a = \sum_{b, c} \epsilon_{a b c} \frac{\partial}{\partial x_b} A_c . \end{displaymath}$

For if has this form, then the left-hand side of Maxwell's equation summarizing Faraday's measurements involving time-dependent magnetic fields, as above, is:

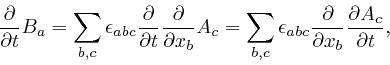
$\begin{displaymath}\frac{\partial}{\partial t} B_a = \sum_{b, c} \epsilon_{a b c... ...frac{\partial}{\partial x_b} \frac{\partial A_c}{\partial t}, \end{displaymath}$

where I assumed that the vector potential depends smoothly on position and time, and used the result we found above. And if has the above form, then the right-hand side of that equation is:

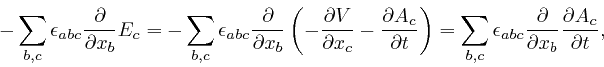
$\begin{displaymath}- \sum_{b, c} \epsilon_{a b c} \frac{\partial}{\partial x_b} ... ...frac{\partial}{\partial x_b} \frac{\partial A_c}{\partial t}, \end{displaymath}$

where I again used the result we found above. This is equal to the left-hand side as above, so if and are derived from a voltage field and a vector potential field as above, then Maxwell's equation summarizing Faraday's measurements involving time-dependent magnetic fields, as above, is solved.

And if the magnetic induction field is derived from a vector potential field as above, then the left-hand side of Maxwell's equation above summarizing the non-observation of magnetic monopoles is:

$\begin{displaymath}\sum_a \frac{\partial}{\partial x_a} B_a = \sum_a \frac{\part... ...artial}{\partial x_a} \frac{\partial}{\partial x_b} A_c = 0, \end{displaymath}$

by a similar calculation to the one above. Thus Maxwell's equation summarizing the non-observation of magnetic monopoles is also solved.

If the electric field strength and the magnetic induction field are derived from a voltage field and a vector potential field , as above, then in a vacuum, where the electric displacement field is related to the electric field strength by $D = \epsilon_0 E$ , and the magnetic field strength is related to the magnetic induction field by $H = \frac{1}{\mu_0} B$ , Maxwell's equation summarizing Coulomb's law, as above, becomes:

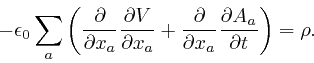
$\begin{displaymath}- \epsilon_0 \sum_a \left( \frac{\partial}{\partial x_a} \fra... ...partial x_a} \frac{\partial A_a}{\partial t} \right) = \rho . \end{displaymath}$

And Maxwell's corrected equation summarizing Ampère's law, as above, becomes:

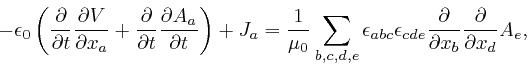
$\begin{displaymath}- \epsilon_0 \left( \frac{\partial}{\partial t} \frac{\partia... ...rac{\partial}{\partial x_b} \frac{\partial}{\partial x_d} A_e, \end{displaymath}$

where each index $a, b, c, d, e, \ldots$ from the start of the lower-case English alphabet can take values 1, 2, 3, corresponding to the directions in which the three Cartesian coordinates of spatial position increase.

To simplify the above formula, we'll consider the expression:

$\begin{displaymath}X_{a b c, d e f} = \delta_{a d} \delta_{b e} \delta_{c f} + \... ..._{b d} \delta_{c f} - \delta_{a f} \delta_{b e} \delta_{c d}, \end{displaymath}$

where $\delta_{a b}$ is the Kronecker delta, that I defined in the first part of the post, here, so its value is 1 when , and 0 otherwise. Thus $\delta_{11} = \delta_{22} = \delta_{33} = 1$ , and $\delta_{12} = \delta_{21} = \delta_{13} = \delta_{31} = \delta_{23} = \delta_{32} = 0$ . A quantity whose value is unchanged if two of its indexes of the same type are swapped is said to be "symmetric" in those indexes, so from the definition of a tensor, as above, $\delta_{a b}$ is an example of a symmetric tensor.

In the above definition of the tensor $X_{a b c, d e f}$ , each term in the right-hand side after the first term is obtained from the first term by leaving the indexes , , and in the same positions as in the first term, and swapping the indexes , , and among themselves. Among the 6 terms in the right-hand side, each of the possible sequences of the letters occurs exactly once, where for each non-negative whole number , I defined in the second part of the post here, and we observed in the second part of the post, here, that the number of different ways of putting distinguishable objects in distinguishable places, such that exactly one object goes to each place, is Thus the number of different sequences of different letters is .

A re-ordering of a sequence of different letters is called a permutation of the sequence. The sign of each term in the right-hand side of the above definition of $X_{a b c, d e f}$ is a sign associated with the permutation that changes the sequence into the sequence in which the letters occur in that term, and is defined in the following way. For any permutation of a sequence of different letters, a cycle of the permutation is a sequence of the letters such that the final position of each letter of the cycle is the same as the initial position of the next letter of the cycle, except that the final position of the last letter of the cycle is the same as the initial position of the first letter of the cycle. For example, for the permutation $d, e, f \rightarrow d, f, e$ , the letter by itself is a cycle, and is a cycle. Two cycles are considered to be equivalent if they have the same letters, and the number of letters in a cycle is called its length. The sign associated with a permutation, which is called the sign of the permutation, is the sign of $\left( - 1 \right)^q$ , where is the number of inequivalent cycles of even length. For example the second term in the right-hand side of the above definition of $X_{a b c, d e f}$ corresponds to the permutation $d, e, f \rightarrow e, f, d$ , which has just one cycle whose length is 3, so its sign is .

If a permutation is followed by another permutation that just swaps two letters, then the cycles of the resulting permutation are the same as the cycles of the original permutation, except that if the two swapped letters were originally in the same cycle, that cycle is divided into two cycles, each of which contains one of the swapped letters, while if the two swapped letters were originally in two different cycles, those two cycles are combined into a single cycle. If the two swapped letters were originally in a cycle of even length, then when that cycle is divided into two cycles, the number of cycles of even length either increases by 1 or decreases by 1, so $\left( - 1 \right)^q$ is multiplied by . If the two swapped letters were originally in a cycle of odd length, then when that cycle is divided into two cycles, one of the resulting cycles has even length and the other has odd length, so the number of cycles of even length increases by 1, so $\left( - 1 \right)^q$ is again multiplied by . And if the two swapped letters were originally in two different cycles then the reverse of one of the preceding cases occurs, so $\left( - 1 \right)^q$ is again multiplied by . Thus swapping any two letters reverses the sign of a permutation.

Thus if any two of the last three indexes of $X_{a b c, d e f}$ are swapped, the value of $X_{a b c, d e f}$ is multiplied by , so in accordance with the definition above, $X_{a b c, d e f}$ is antisymmetric in its last three indexes. Thus the value of $X_{a b c, d e f}$ must be 0 when any two of its last three indexes have the same value, for example $X_{a b c, 1 1 2}$ must be 0, since swapping the 4th and 5th indexes of $X_{a b c, d e f}$ multiplies its value by . The only possible values of each index are 1, 2, or 3, so $X_{a b c, d e f}$ is 0 unless $\left( d, e, f \right)$ is one of the possibilities $\left( 1, 2, 3 \right)$ , $\left( 2, 3, 1 \right)$ , $\left( 3, 1, 2 \right)$ , $\left( 1, 3, 2 \right)$ , $\left( 2, 1, 3 \right)$ , or $\left( 3, 2, 1 \right)$ , and furthermore,

$\begin{displaymath}X_{a b c, 1 2 3} = X_{a b c, 2 3 1} = X_{a b c, 3 1 2} = - X_{a b c, 1 3 2} = - X_{a b c, 2 1 3} = - X_{a b c, 3 2 1} . \end{displaymath}$

From the definition of the antisymmetric tensor $\epsilon_{a b c}$ , as above, this implies that:

$\begin{displaymath}X_{a b c, d e f} = X_{a b c, 1 2 3} \epsilon_{d e f}, \end{displaymath}$

since this equation is true for $\left( d, e, f \right) = \left( 1, 2, 3 \right)$ because $\epsilon_{1 2 3} = 1$ , and it is therefore also true for all the other values of $\left( d, e, f \right)$ for which $X_{a b c, d e f}$ is non-zero, by the preceding equation and the definition of $\epsilon_{a b c}$ , as above, and it is also true whenever two of the indexes have the same value, since both sides of the equation are then 0.

We can also write the definition above of $X_{a b c, d e f}$ as:

$\begin{displaymath}X_{a b c, d e f} = \delta_{a d} \delta_{b e} \delta_{c f} + \... ..._{a e} \delta_{c f} - \delta_{c d} \delta_{b e} \delta_{a f}, \end{displaymath}$

which is the same as the formula above, except that I have changed the order of the factors in each term after the first, so that the indexes now occur in the same order in every term, while the order of the indexes is now different in each term. Each term now corresponds to one of the 6 permutations of the letters , and the sign of each term is the sign of the corresponding permutation of the letters . So in the same way as above, we find that $X_{a b c, d e f}$ is also antisymmetric in its first three indexes, and that:

$\begin{displaymath}X_{a b c, d e f} = \epsilon_{a b c} X_{1 2 3, d e f} . \end{displaymath}$

From this and the formula above, we find:

$\begin{displaymath}X_{a b c, d e f} = \epsilon_{a b c} X_{1 2 3, d e f} = X_{a b c, 1 2 3} \epsilon_{d e f} . \end{displaymath}$

This is true for all cases where the indexes take values 1, 2, or 3, and from the case where $\left( a, b, c \right) = \left( 1, 2, 3 \right)$ , we find:

$\begin{displaymath}X_{1 2 3, d e f} = X_{1 2 3, 1 2 3} \epsilon_{d e f} . \end{displaymath}$

Thus:

$\begin{displaymath}X_{a b c, d e f} = \epsilon_{a b c} X_{1 2 3, d e f} = X_{1 2 3, 1 2 3} \epsilon_{a b c} \epsilon_{d e f} . \end{displaymath}$

Furthermore, $X_{1 2 3, 1 2 3} = 1$ , since for these values of the indexes, only the first term in the right-hand side of the above definition of $X_{a b c, d e f}$ is non-zero, and its value is 1. Thus $X_{a b c, d e f} = \epsilon_{a b c} \epsilon_{d e f}$ , so:

$\begin{displaymath}\epsilon_{a b c} \epsilon_{d e f} = \delta_{a d} \delta_{b e}... ..._{b d} \delta_{c f} - \delta_{a f} \delta_{b e} \delta_{c d} . \end{displaymath}$

We now observe that:

$\begin{displaymath}\sum_c \delta_{c c} = \delta_{11} + \delta_{22} + \delta_{33} = 3, \end{displaymath}$

and

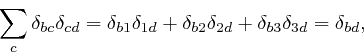
$\begin{displaymath}\sum_c \delta_{b c} \delta_{c d} = \delta_{b 1} \delta_{1 d} ... ...b 2} \delta_{2 d} + \delta_{b 3} \delta_{3 d} = \delta_{b d}, \end{displaymath}$

since the indexes and can take values 1, 2, or 3, and from the definition of the Kronecker delta in the first part of the post, here, the product $\delta_{b c} \delta_{c d}$ is non-zero for exactly one value of if , namely for , in which case $\delta_{b c} \delta_{c d} = 1$ , while if $b \neq d$ , where the symbol $\neq$ means, "is not equal to," then $\delta_{b c}$ and $\delta_{c d}$ are not both non-zero for any value of .

Thus:

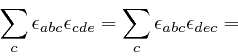
$\begin{displaymath}\sum_c \epsilon_{a b c} \epsilon_{c d e} = \sum_c \epsilon_{a b c} \epsilon_{d e c} = \end{displaymath}$

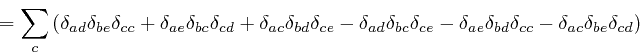
$\begin{displaymath}= \sum_c \left( \delta_{a d} \delta_{b e} \delta_{c c} + \del... ... \delta_{c c} - \delta_{a c} \delta_{b e} \delta_{c d} \right) \end{displaymath}$

$\begin{displaymath}= 3 \delta_{a d} \delta_{b e} + \delta_{a e} \delta_{b d} + \... ... e} - 3 \delta_{a e} \delta_{b d} - \delta_{a d} \delta_{b e} \end{displaymath}$

$\begin{displaymath}= \left( 3 - 1 - 1 \right) \delta_{a d} \delta_{b e} + \left( 1 + 1 - 3 \right) \delta_{a e} \delta_{b d} \end{displaymath}$

$\begin{displaymath}= \delta_{a d} \delta_{b e} - \delta_{a e} \delta_{b d} . \end{displaymath}$

Thus Maxwell's corrected equation summarizing Ampère's law, as above, expressed in terms of the voltage field and the vector potential field , as above, is:

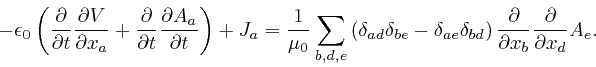
$\begin{displaymath}- \epsilon_0 \left( \frac{\partial}{\partial t} \frac{\partia... ...{\partial}{\partial x_b} \frac{\partial}{\partial x_d} A_e . \end{displaymath}$

We now observe that for any vector :

$\begin{displaymath}\sum_b \delta_{a b} X_b = \delta_{a 1} X_1 + \delta_{a 2} X_2 + \delta_{a 3} X_3 = X_a, \end{displaymath}$

since $\delta_{a b}$ is non-zero for exactly one value of , namely for , in which case it is 1.

Using this property of the Kronecker delta, we find:

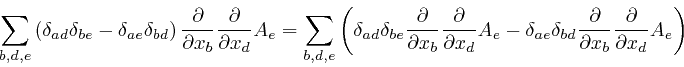
$\begin{displaymath}\sum_{b, d, e} \left( \delta_{a d} \delta_{b e} - \delta_{a e... ...rtial}{\partial x_b} \frac{\partial}{\partial x_d} A_e \right) \end{displaymath}$

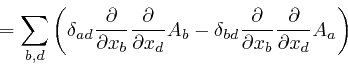
$\begin{displaymath}= \sum_{b, d} \left( \delta_{a d} \frac{\partial}{\partial x_... ...tial}{\partial x_b} \frac{\partial}{\partial x_d} A_a \right) \end{displaymath}$

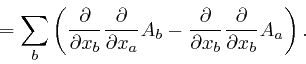
$\begin{displaymath}= \sum_b \left( \frac{\partial}{\partial x_b} \frac{\partial}... ...al}{\partial x_b} \frac{\partial}{\partial x_b} A_a \right) . \end{displaymath}$

Thus Maxwell's corrected equation summarizing Ampère's law, as above, expressed in terms of the voltage field and the vector potential field , as above, is:

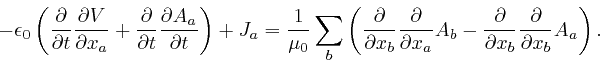
$\begin{displaymath}- \epsilon_0 \left( \frac{\partial}{\partial t} \frac{\partia... ...l}{\partial x_b} \frac{\partial}{\partial x_b} A_a \right) . \end{displaymath}$

We now observe that the formulae for the electric field strength and the magnetic induction field in terms of the voltage field and the vector potential field , as above, are unaltered if and are modified by the following replacements:

$\begin{displaymath}V \rightarrow V' = V - \frac{\partial}{\partial t} f, \hspace... ...A_a \rightarrow A'_a = A_a + \frac{\partial}{\partial x_a} f, \end{displaymath}$

where is an arbitrary scalar field that depends smoothly on position and time. For the modified electric field strength and magnetic induction field are:

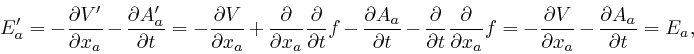
$\begin{displaymath}E'_a = - \frac{\partial V'}{\partial x_a} - \frac{\partial A'... ...tial V}{\partial x_a} - \frac{\partial A_a}{\partial t} = E_a, \end{displaymath}$

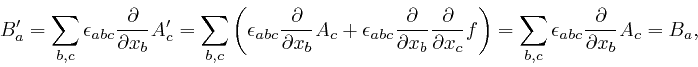
$\begin{displaymath}B'_a = \sum_{b, c} \epsilon_{a b c} \frac{\partial}{\partial ... ... c} \epsilon_{a b c} \frac{\partial}{\partial x_b} A_c = B_a, \end{displaymath}$

where I used the result we found above, and a similar calculation to the one above.

The replacement of the voltage field and the vector potential field by modified fields and , as above, which leaves the electric field strength and the magnetic induction field unaltered, and thus has no experimentally observable consequences, is called a gauge transformation.

We can simplify Maxwell's equation summarizing Coulomb's law, and his corrected equation summarizing Ampère's law, expressed in terms of the voltage field and the vector potential field , as above, and above, by doing a gauge transformation with a scalar field that satisfies:

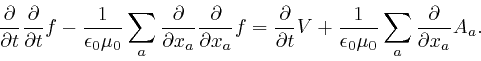
$\begin{displaymath}\frac{\partial}{\partial t} \frac{\partial}{\partial t} f - ... ...}{\epsilon_0 \mu_0} \sum_a \frac{\partial}{\partial x_a} A_a . \end{displaymath}$

We then find that:

$\begin{displaymath}\frac{\partial V'}{\partial t} + \frac{1}{\epsilon_0 \mu_0} \... ...ial x_a} \left( A_a + \frac{\partial}{\partial x_a} f \right) \end{displaymath}$

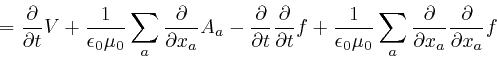
$\begin{displaymath}= \frac{\partial}{\partial t} V + \frac{1}{\epsilon_0 \mu_0} ... ... \frac{\partial}{\partial x_a} \frac{\partial}{\partial x_a} f \end{displaymath}$

$\begin{displaymath}= 0. \end{displaymath}$

Let's now assume that we've done a gauge transformation as above, so that:

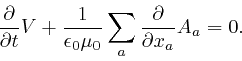
$\begin{displaymath}\frac{\partial}{\partial t} V + \frac{1}{\epsilon_0 \mu_0} \sum_a \frac{\partial}{\partial x_a} A_a = 0. \end{displaymath}$

This is called a gauge condition.

Then by the result we found above, the term $- \epsilon_0 \sum_a \frac{\partial}{\partial x_a} \frac{\partial A_a}{\partial t}$ in the left-hand side of Maxwell's equation summarizing Coulomb's law, expressed in terms of the voltage field and the vector potential field , as above, is equal to $\epsilon^2_0 \mu_0 \frac{\partial}{\partial t} \frac{\partial V}{\partial t}$ , so that equation becomes:

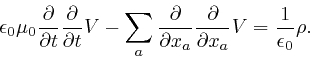
$\begin{displaymath}\epsilon_0 \mu_0 \frac{\partial}{\partial t} \frac{\partial}{... ...\frac{\partial}{\partial x_a} V = \frac{1}{\epsilon_0} \rho . \end{displaymath}$

And Maxwell's corrected equation summarizing Ampère's law, expressed in terms of the voltage field and the vector potential field , as above, becomes:

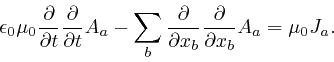
$\begin{displaymath}\epsilon_0 \mu_0 \frac{\partial}{\partial t} \frac{\partial}{... ...\partial x_b} \frac{\partial}{\partial x_b} A_a = \mu_0 J_a . \end{displaymath}$

Let's now consider a region where there are no electrically charged particles and no electric currents, so that $\rho$ and are 0. Then for any vector , and any angle $\theta$ , and any vector perpendicular to , which from the discussion above, means that $\sum_a P_a k_a = 0$ , a solution of the above equations that satisfies the gauge condition above, which we used to simplify the equations, is given by:

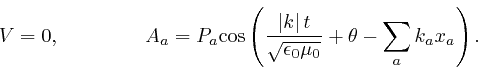
$\begin{displaymath}V = 0, \hspace{1.5cm} A_a = P_a \mathrm{\cos} \left( \frac{\l... ...}{\sqrt{\epsilon_0 \mu_0}} + \theta - \sum_a k_a x_a \right) . \end{displaymath}$

For we found in the first part of the post, here, that $\frac{\mathrm{d}}{\mathrm{d} y} \mathrm{\cos} \left( y \right) = - \mathrm{\sin} \left( y \right)$ and $\frac{\mathrm{d}}{\mathrm{d} y} \mathrm{\sin} \left( y \right) = \mathrm{\cos} \left( y \right)$ . So by a calculation similar to the one in the second part of the post, here, if and are any quantities independent of , then $\frac{\mathrm{d}}{\mathrm{d} y} \mathrm{\cos} \left( py + q \right) = - p \mathrm{\sin} \left( py + q \right)$ and $\frac{\mathrm{d}}{\mathrm{d} y} \mathrm{\sin} \left( py + q \right) = p \mathrm{\cos} \left( py + q \right)$ . From these results with taken as and , we find:

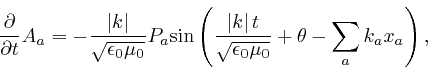
$\begin{displaymath}\frac{\partial}{\partial t} A_a = - \frac{\left\vert k \righ... ...t}{\sqrt{\epsilon_0 \mu_0}} + \theta - \sum_a k_a x_a \right), \end{displaymath}$

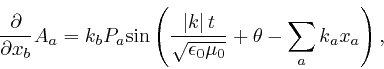
$\begin{displaymath}\frac{\partial}{\partial x_b} A_a = k_b P_a \mathrm{\sin} \le... ...}{\sqrt{\epsilon_0 \mu_0}} + \theta - \sum_a k_a x_a \right), \end{displaymath}$

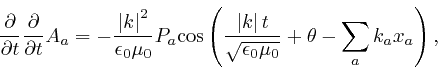
$\begin{displaymath}\frac{\partial}{\partial t} \frac{\partial}{\partial t} A_a =... ...}{\sqrt{\epsilon_0 \mu_0}} + \theta - \sum_a k_a x_a \right), \end{displaymath}$

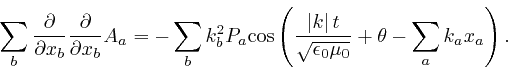
$\begin{displaymath}\sum_b \frac{\partial}{\partial x_b} \frac{\partial}{\partial... ...}{\sqrt{\epsilon_0 \mu_0}} + \theta - \sum_a k_a x_a \right) . \end{displaymath}$

From the second of these results, we find that $\sum_a \frac{\partial}{\partial x_a} A_a$ is proportional to $\sum_a P_a k_a = 0$ , so the gauge condition above is satisfied, and since $\left\vert k \right\vert = \sqrt{\sum_b k^2_b}$ by Pythagoras, the third and fourth of these results show that Maxwell's equation summarizing Ampère's law, as above, is satisfied. Maxwell's equation summarizing Coulomb's law, as above, is automatically satisfied, since for this solution.

From the formulae for the electric field strength and the magnetic induction field in terms of the voltage field and the vector potential field , as above, we find that for this solution:

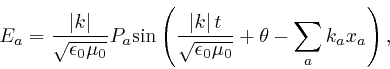
$\begin{displaymath}E_a = \frac{\left\vert k \right\vert}{\sqrt{\epsilon_0 \mu_0}... ...}{\sqrt{\epsilon_0 \mu_0}} + \theta - \sum_a k_a x_a \right), \end{displaymath}$

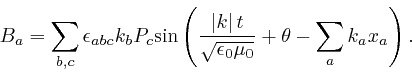
$\begin{displaymath}B_a = \sum_{b, c} \epsilon_{a b c} k_b P_c \mathrm{\sin} \lef... ...{\sqrt{\epsilon_0 \mu_0}} + \theta - \sum_a k_a x_a \right) . \end{displaymath}$

Thus since we assumed that $\sum_a P_a k_a = 0$ , we find that $\sum_a E_a k_a = 0$ , which from the discussion above means that the vector is perpendicular to the vector . And from calculations similar to the one above we find that $\sum_{a, b, c} \epsilon_{a b c} k_b P_c k_a = 0$ , so that $\sum_a B_a k_a = 0$ , so the vector is perpendicular to the vector , and $\sum_{a, b, c} P_a \epsilon_{a b c} k_b P_c = 0$ , so $\sum_a E_a B_a = 0$ , so the electric field strength is perpendicular to the magnetic induction field .

This solution describes oscillating electric and magnetic fields moving in the direction at a speed $\frac{1}{\sqrt{\epsilon_0 \mu_0}}$ . From above, the permittivity $\epsilon_0$ of a vacuum, measured from the electric charge stored on a paralle plate capacitor, is such that:

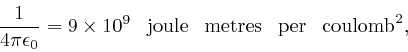
$\begin{displaymath}\frac{1}{4 \pi \epsilon_0} = 9 \times 10^9 \hspace{0.8em} \m... ...8em} \mathrm{{{per}}} \hspace{0.8em} \mathrm{{{coulomb}}}^2, \end{displaymath}$

and from above, the definition of one amp one coulomb per second, in terms of the force between long parallel wires carrying steady electric currents, as above, implies that the permeability $\mu_0$ of a vacuum is by definition given by:

$\begin{displaymath}\mu_0 = 4 \pi \times 10^{- 7} \hspace{0.8em} \mathrm{{{kilog... ...em} \mathrm{{{per}}} \hspace{0.8em} \mathrm{{{coulomb}}}^2 . \end{displaymath}$

Thus:

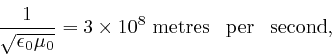
$\begin{displaymath}\frac{1}{\sqrt{\epsilon_0 \mu_0}} = 3 \times 10^8 \; \mathrm... ...{0.8em} \mathrm{{{per}}} \hspace{0.8em} \mathrm{{{second}}}, \end{displaymath}$

which is the measured value of the speed of light. Maxwell therefore proposed that light is waves of oscillating electric and magnetic fields perpendicular to the direction of motion of the wave and to each other. The vector is called the wave vector, and the wave solutions above are called transverse waves, because the vector potential is perpendicular to the wave vector .

From calculations similar to those above, we find that the gauge condition above, and the field equations above, have another wave solution:

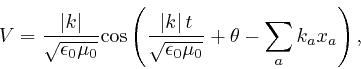
$\begin{displaymath}V = \frac{\left\vert k \right\vert}{\sqrt{\epsilon_0 \mu_0}} ... ...}{\sqrt{\epsilon_0 \mu_0}} + \theta - \sum_a k_a x_a \right), \end{displaymath}$

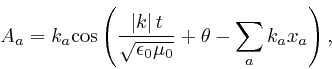
$\begin{displaymath}A_a = k_a \mathrm{\cos} \left( \frac{\left\vert k \right\vert t}{\sqrt{\epsilon_0 \mu_0}} + \theta - \sum_a k_a x_a \right), \end{displaymath}$

which is called a longitudinal wave, because the vector potential is parallel to the wave vector . However from the formulae for the electric field strength and the magnetic induction field in terms of the voltage field and the vector potential field , as above, we find that for this solution:

$\begin{displaymath}E_a = 0, \hspace{1.5cm} B_a = 0. \end{displaymath}$

Thus the above longitudinal wave solution has no experimentally observable effects. It is called a pure gauge mode.

Maxwell suggested that there could also be transverse waves of electric and magnetic fields with frequencies outside the visible spectrum, and this was partly confirmed in 1879 by experiments by David Edward Hughes, and conclusively confirmed in 1886 when Heinrich Hertz generated and detected pulses of radio-frequency electromagnetic waves in his laboratory. This led to the utilization of radio-frequency electromagnetic waves for practical communications by Guglielmo Marconi, from around 1895.

Electromagnetic waves will also be emitted by hot objects, and will be present in a hot region that is in thermal equilibrium. It was the study of the electromagnetic waves in hot ovens, at the end of the nineteenth century, that provided the other part of the clue that led to the discovery of quantum mechanics and Richard Feynman's functional integral. In the next part of this post, Action for Fields, we'll look at how Maxwell's equations for the for the electric field strength and the magnetic induction field , expressed in terms of the voltage field and the vector potential field , as above, can be obtained from de Maupertuis's principle of stationary action, for a suitable action that depends on the electromagnetic fields and , and on the positions and motions of any electrically charged particles present, and in the part after that, Radiation in an Oven, we'll look at how the discoveries about heat and temperature that we looked at in the second part of this post, combined with the discoveries about electromagnetic radiation that we've looked at today, lead to a seriously wrong conclusion about the properties of electromagnetic radiation in a hot oven. In the subsequent parts of the post, we'll look at how that problem has been resolved by the discovery of quantum mechanics and Feynman's functional integral, which started with the identification of a new fundamental constant of nature by Max Planck, in 1899.

The software on this website is licensed for use under the Free Software Foundation General Public License.

Page last updated 28 November 2020. Copyright (c) Chris Austin 2012 - 2020. Privacy policy