Home Blog index Previous Next About Privacy policy

banner

Dirac-Feynman-Berezin sums 5 - Radiation in an oven

By Chris Austin. 30 November 2020.

An earlier version of this post was published on another website on 1 January 2013.

This is the fifth in a series of posts about the foundation of our understanding of the way the physical world works, which I'm calling Dirac-Feynman-Berezin sums. The previous post in the series is Action For Fields.

As in the previous posts, I'll show you some formulae and things like that along the way, but I'll try to explain what all the parts mean as we go along, if we've not met them already, so you don't need to know about that sort of thing in advance.

One of the clues that led to the discovery of Dirac-Feynman-Berezin sums came from the attempted application to electromagnetic radiation of discoveries about heat and temperature. We looked at those discoveries about heat and temperature in the second post in the series, and in the third post, we looked at how James Clerk Maxwell, just after the middle of the nineteenth century, was able to identify light as waves of oscillating electric and magnetic fields, and to calculate the speed of light from measurements of electrical and magnetic effects. Dirac-Feynman-Berezin sums for a physical system depend on a property of the system called its action, and in the first post in the series, we derived Sir Isaac Newton's second law of motion from Pierre-Louis de Maupertuis's principle of stationary action. In the fourth post, we calculated the conserved energy of a system of electromagnetic fields and electrically charged particles, by deriving Maxwell's equations for the electromagnetic fields, and the forces exerted on the charged particles by the fields, from de Maupertuis's principle for the action of the system.

Today I would like to put all these pieces together, and show you how they led to a seriously wrong conclusion about the properties of electromagnetic radiation in a hot oven. In the next post in the series, Dirac-Feynman sums, we'll look at how the problem was resolved by the discoveries that led to Dirac-Feynman-Berezin sums, which started with the identification of a new fundamental constant of nature by Max Planck, in 1899.

Let's now consider the electromagnetic fields in a box-shaped oven whose sides are aligned with the Cartesian coordinate directions, and whose internal dimensions in the Cartesian coordinate directions are $L_1$, $L_2$, and $L_3$. We'll assume that the internal faces of the oven walls are perfectly reflecting, and that the oven is empty apart from the electromagnetic fields. We found in the third post in the series, here, that for any vector $k$, any angle $\theta$, and any vector $P$ perpendicular to $k$, which means that $\sum_a P_a k_a = 0$, a solution of the equations for the electromagnetic field in a vacuum, with no electric charges or electric currents present, is given by:

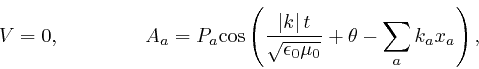
\begin{displaymath}V = 0, \hspace{1.5cm} A_a = P_a \mathrm{\cos} \left( \frac{\l... ...t}{\sqrt{\epsilon_0 \mu_0}} + \theta - \sum_a k_a x_a \right), \end{displaymath}

where $V$ is the voltage field and $A$ is the vector potential field, and the electric field strength $E$ and the magnetic induction field $B$ are expressed in terms of $V$ and $A$ by the formulae we found in the third post in the series, here. We found in the third post in the series, here, that $\frac{1}{\sqrt{\epsilon_0 \mu_0}}$ is equal to the speed of light $c = 3.0 \times 10^8$ metres per second in a vacuum, so I'll now write $c$ instead of $\frac{1}{\sqrt{\epsilon_0 \mu_0}}$.

From calculations similar to the ones in the third post in the series, here, which confirmed that a wave of the above form satisfies the gauge condition on $V$ and $A$ in the third post in the series, here, and Maxwell's equations in a vacuum in terms of $V$ and $A$ assuming that gauge condition, as in the third post in the series, here, with no electric charges or electric currents present, we find that an arbitrary sum of waves of the above form also satisfies those equations. We'll assume that the electromagnetic fields inside the oven consist of a sum of waves of the above form, so that $V = 0$ inside the oven.

Maxwell's equation summarizing Faraday's measurements involving time-dependent magnetic fields, as in the third post in the series, here, shows that the components of $E$ tangential to an oven wall must be continuous at the oven wall, for if a component of $E$ tangential to the oven wall changed discontinously at the oven wall, the component of $\frac{\partial B}{\partial t}$ in the perpendicular direction along the oven wall would have to be infinite at the oven wall. The assumption that the oven walls are perfectly reflecting means that $E$ and $B$ are 0 inside the material of the oven walls, and we'll assume that $V$ and $A$ are also 0 inside the material of the oven walls. So from the formula for $E$ in terms of $V$ and $A$, as in the third post in the series, here, the tangential components of $A$ must be continuous at the oven wall, and are thus 0 at the oven wall.

The requirement that the tangential components of $A$ must be 0 at each wall of the oven is called a boundary condition, and restricts the possible wave vectors $k$ of the electromagnetic waves inside the oven. We'll assume that the interior faces of the oven walls perpendicular to the $a$ Cartesian coordinate direction are at $x_a = 0$ and $x_a = L_a$, for $a = 1, 2, 3$. A single wave of the above form with a nonzero polarization vector $P$ and a nonzero wave vector $k$ cannot satisfy the boundary condition on any wall of the oven by itself, so if there is a wave present with particular values of $k$, $P$, and $\theta$, there must also be other waves present with different values of $k$, $P$, or $\theta$, such that the sum of these waves satisfies the boundary conditions.

Considering first the boundary at $x_1 = 0$, if there is a wave present with

\begin{displaymath}A_a = P_a \mathrm{\cos} \left( c \left\vert k \right\vert t + \theta - k_1 x_1 - k_2 x_2 - k_3 x_3 \right), \end{displaymath}

with nonzero $P$ and $k$, then there must also be other waves present with different values of $k$, $P$, or $\theta$, such that the sum of $P_a \mathrm{\cos} \left( c \left\vert k \right\vert t + \theta - k_2 x_2 - k_3 x_3 \right)$ over these waves is 0 for all values of $t$, and all values of $x_2$ in the range $0 \leq x_2 \leq L_2$, and all values of $x_3$ in the range $0 \leq x_3 \leq L_3$. Any waves present relevant to satisfying the boundary condition at $x_1 = 0$ will have the same values of $k_2$, $k_3$, and $\left\vert k \right\vert$, and we can also require them to have the same value of $\theta$, since from the first post in the series, here, the value of $\mathrm{\cos} \left( y \right)$ is unaltered by adding a whole number times $2 \pi$ to $y$. Thus since $\left\vert k \right\vert = \sqrt{k^2_1 + k^2_2 + k^2_3}$, the only other relevant value of $k_1$ is $- k_1$. Thus to satisfy the boundary condition at $x_1 = 0$, any wave present as above must be paired with another wave with the opposite value of $k_1$, such that the sum of the two waves has the form:

\begin{displaymath}A_a = \left( P_1, P_2, P_3 \right) \mathrm{\cos} \left( c \le... ... \right\vert t + \theta - k_1 x_1 - k_2 x_2 - k_3 x_3 \right) \end{displaymath}

\begin{displaymath}- \left( - P_1, P_2, P_3 \right) \mathrm{\cos} \left( c \left... ...\right\vert t + \theta + k_1 x_1 - k_2 x_2 - k_3 x_3 \right), \end{displaymath}

since the 2 and 3 components of this are 0 at $x_1 = 0$, and the polarization vector $- \left( - P_1, P_2, P_3 \right)$ of the second wave is perpendicular to the wave vector $\left( - k_1, k_2, k_3 \right)$ of the second wave.

Considering, next, the boundary condition at $x_1 = L_1$, this must also be satisfied by the above sum of two waves, since any relevant waves have the same values of $k_2$, $k_3$, and $\left\vert k \right\vert$, and can be chosen to have the same value of $\theta$. Thus we require $k$, $P$, and $\theta$ to be such that the 2 and 3 components of the above sum of two waves are also 0 at $x_1 = L_1$, for all values of $t$, and all values of $x_2$ in the range $0 \leq x_2 \leq L_2$, and all values of $x_3$ in the range $0 \leq x_3 \leq L_3$. To determine the values of $k$, $P$, and $\theta$ that satisfy this requirement, it is helpful to know about a formula that expresses $\mathrm{\cos} \left( \theta_1 + \theta_2 \right)$ in terms of $\mathrm{\cos} \left( \theta_1 \right)$, $\mathrm{\cos} \left( \theta_2 \right)$, $\mathrm{\sin} \left( \theta_1 \right)$, and $\mathrm{\sin} \left( \theta_2 \right)$, for arbitrary angles $\theta_1$ and $\theta_2$.

From the definition of $\mathrm{\cos} \left( \theta \right)$ and $\mathrm{\sin} \left( \theta \right)$, as in the first post in the series, here, $\left( \mathrm{\cos} \left( \theta_1 \right), \mathrm{\sin} \left( \theta_1 \right) \right)$ are the Cartesian coordinates, in the 2-dimensional plane of Euclidean geometry, of a point that is moving along a circle of radius 1 centred at the point with Cartesian coordinates $\left( 0, 0 \right)$, such that the angle between the straight line from $\left( 0, 0 \right)$ to $\left( \mathrm{\cos} \left( \theta_1 \right), \mathrm{\sin} \left( \theta_1 \right) \right)$ and the straight line from $\left( 0, 0 \right)$ to $\left( 1, 0 \right)$ is $\theta_1$, and $\frac{\mathrm{d}}{\mathrm{d} \theta_1} \mathrm{\sin} \left( \theta_1 \right)$ is $> 0$ at $\theta_1 = 0$. We'll now use the straight line from $\left( 0, 0 \right)$ to $\left( \mathrm{\cos} \left( \theta_1 \right), \mathrm{\sin} \left( \theta_1 \right) \right)$ as the first coordinate direction of a second set of Cartesian coordinates also centred at $\left( 0, 0 \right)$, such that the coordinate directions of the second set of Cartesian coordinates rotate into the original set as $\theta_1$ tends to 0. From the definition of Cartesian coordinates, as in the first post in the series, here, the second coordinate direction $\left( x_1, x_2 \right)$ of the second set of Cartesian coordinates must be perpendicular to the first coordinate direction of the second set, so by the discussion in the third post in the series, here, it satisfies $x_1 \mathrm{\cos} \left( \theta_1 \right) + x_2 \mathrm{\sin} \left( \theta_1 \right) = 0$, whose solution of length 1 is $\left( x_1, x_2 \right) = \pm \left( - \mathrm{\sin} \left( \theta_1 \right), \mathrm{\cos} \left( \theta_1 \right) \right)$. This is required to become $\left( 0, 1 \right)$ as $\theta_1$ tends to 0, so the required solution is $\left( x_1, x_2 \right) = \left( - \mathrm{\sin} \left( \theta_1 \right), \mathrm{\cos} \left( \theta_1 \right) \right)$. A point whose coordinates are $\left( \mathrm{\cos} \left( \theta_1 + \theta_2 \right), \mathrm{\sin} \left( \theta_1 + \theta_2 \right) \right)$ with respect to the first set of coordinates has coordinates $\left( \mathrm{\cos} \left( \theta_2 \right), \mathrm{\sin} \left( \theta_2 \right) \right)$ with respect to the second set of coordinates, so we have:

\begin{displaymath}\left( \mathrm{\cos} \left( \theta_1 + \theta_2 \right), \mat... ...heta_1 \right), \mathrm{\cos} \left( \theta_1 \right) \right) \end{displaymath}

\begin{displaymath}= \left( \mathrm{\cos} \left( \theta_2 \right) \mathrm{\cos} ... ...eta_2 \right) \mathrm{\cos} \left( \theta_1 \right) . \right. \end{displaymath}

Thus we have:

\begin{displaymath}\mathrm{\cos} \left( \theta_1 + \theta_2 \right) = \mathrm{\c... ...\left( \theta_1 \right) \mathrm{\sin} \left( \theta_2 \right), \end{displaymath}

and also:

\begin{displaymath}\mathrm{\sin} \left( \theta_1 + \theta_2 \right) = \mathrm{\s... ...\left( \theta_1 \right) \mathrm{\sin} \left( \theta_2 \right), \end{displaymath}

for all angles $\theta_1$ and all angles $\theta_2$.

The above sum of two waves is therefore equal to:

\begin{displaymath}A_a = \left( P_1, P_2, P_3 \right) \left( \mathrm{\cos} \left... ... \alpha \right) \mathrm{\sin} \left( - k_1 x_1 \right) \right) \end{displaymath}

\begin{displaymath}- \left( - P_1, P_2, P_3 \right) \left( \mathrm{\cos} \left( ... ... \alpha \right) \mathrm{\sin} \left( k_1 x_1 \right) \right), \end{displaymath}

where I have defined the Greek letter $\alpha$ to be $\alpha = c \left\vert k \right\vert t + \theta - k_2 x_2 - k_3 x_3$. We observe from the definition of $\mathrm{\cos} \left( \theta \right)$ and $\mathrm{\sin} \left( \theta \right)$, as in the first post in the series, here, that:

\begin{displaymath}\mathrm{\cos} \left( - \theta \right) = \mathrm{\cos} \left( \theta \right), \end{displaymath}

and:

\begin{displaymath}\mathrm{\sin} \left( - \theta \right) = - \mathrm{\sin} \left( \theta \right), \end{displaymath}

for all $\theta$, so the above sum of two waves is:

\begin{displaymath}A_a = \left( P_1, P_2, P_3 \right) \left( \mathrm{\cos} \left... ...( \alpha \right) \mathrm{\sin} \left( k_1 x_1 \right) \right) \end{displaymath}

\begin{displaymath}- \left( - P_1, P_2, P_3 \right) \left( \mathrm{\cos} \left( ... ...( \alpha \right) \mathrm{\sin} \left( k_1 x_1 \right) \right) \end{displaymath}

\begin{displaymath}= 2 \left( P_1, 0, 0 \right) \mathrm{\cos} \left( \alpha \rig... ...} \left( \alpha \right) \mathrm{\sin} \left( k_1 x_1 \right) . \end{displaymath}

Thus the requirement that the 2 and 3 components of the sum of the two waves are 0 at $x_1 = L_1$, for all values of $t$, and all values of $x_2$ in the range $0 \leq x_2 \leq L_2$, and all values of $x_3$ in the range $0 \leq x_3 \leq L_3$, or equivalently, at $x_1 = L_1$, for all values of $\alpha$, means that either $P_2 = P_3 = 0$, or $\mathrm{\sin} \left( k_1 L_1 \right) = 0$. If $P_2 = P_3 = 0$, then $\sum_a P_a k_a = 0$ and $P_1 \neq 0$ means that $k_1 = 0$, while if $\mathrm{\sin} \left( k_1 L_1 \right) = 0$, then from the definition of $\mathrm{\sin} \left( \theta \right)$, as in the first post in the series, here, we have $k_1 L_1 = \pi n$, for some whole number $n$.

Considering the boundary conditions at the oven walls perpendicular to the 2 and 3 coordinate directions in the same way, we therefore find that if there is a wave present as above with nonzero $P$ and $k$ such that $\sum_a P_a k_a = 0$, then it must be part of a sum of waves of the form:

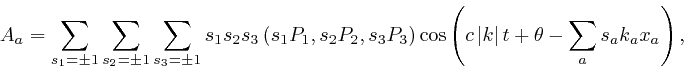
\begin{displaymath}A_a = \sum_{s_1 = \pm 1} \sum_{s_2 = \pm 1} \sum_{s_3 = \pm 1... ...t\vert k \right\vert t + \theta - \sum_a s_a k_a x_a \right), \end{displaymath}

and the components of $k$ must be of the form $k_a = \frac{\pi n_a}{L_a}$, for some whole numbers $n_a$, $a = 1, 2, 3$. Doing the sums over the signs $s_1$, $s_2$, and $s_3$ using the formulae above, we find:

\begin{displaymath}A_1 = - 8 P_1 \mathrm{\cos} \left( c \left\vert k \right\vert... ... \left( k_2 x_2 \right) \mathrm{\sin} \left( k_3 x_3 \right), \end{displaymath}

\begin{displaymath}A_2 = - 8 P_2 \mathrm{\cos} \left( c \left\vert k \right\vert... ... \left( k_2 x_2 \right) \mathrm{\sin} \left( k_3 x_3 \right), \end{displaymath}

\begin{displaymath}A_3 = - 8 P_3 \mathrm{\cos} \left( c \left\vert k \right\vert... ...\left( k_2 x_2 \right) \mathrm{\cos} \left( k_3 x_3 \right) . \end{displaymath}

From the definition of $\mathrm{\cos} \left( \theta \right)$ and $\mathrm{\sin} \left( \theta \right)$, as in the first post in the series, here, we observe that $\mathrm{\cos} \left( \alpha - \frac{\pi}{2} \right) = \mathrm{\sin} \left( \alpha \right)$, for all $\alpha$. Thus from the formula above, we have:

\begin{displaymath}\mathrm{\cos} \left( \alpha + \theta \right) = \mathrm{\cos} ... ... \right) \mathrm{\cos} \left( \alpha - \frac{\pi}{2} \right), \end{displaymath}

for all $\alpha$ and all $\theta$. Thus if we display the $\theta$-dependence of the above sum of waves by representing it as $A_a \left( \theta \right)$, we have:

\begin{displaymath}A_a \left( \theta \right) = \mathrm{\cos} \left( \theta \righ... ...n} \left( \theta \right) A_a \left( - \frac{\pi}{2} \right) . \end{displaymath}

Thus for arbitrary $\theta$, the above sum of waves is equal to a sum of waves of the above form with $\theta = 0$, plus a sum of waves of the above form with $\theta = - \frac{\pi}{2}$.

From the formulae in the third post in the series, here, the electric field strength $E$ and the magnetic induction field $B$ for the above sum of waves are:

\begin{displaymath}E_1 = - 8 c \left\vert k \right\vert P_1 \mathrm{\sin} \left(... ... \left( k_2 x_2 \right) \mathrm{\sin} \left( k_3 x_3 \right), \end{displaymath}

\begin{displaymath}E_2 = - 8 c \left\vert k \right\vert P_2 \mathrm{\sin} \left(... ... \left( k_2 x_2 \right) \mathrm{\sin} \left( k_3 x_3 \right), \end{displaymath}

\begin{displaymath}E_3 = - 8 c \left\vert k \right\vert P_3 \mathrm{\sin} \left(... ... \left( k_2 x_2 \right) \mathrm{\cos} \left( k_3 x_3 \right), \end{displaymath}

\begin{displaymath}B_1 = - 8 \left( k_2 P_3 - k_3 P_2 \right) \mathrm{\cos} \lef... ...} \left( k_2 x_2 \right) \mathrm{\cos} \left( k_3 x_3 \right), \end{displaymath}

\begin{displaymath}B_2 = - 8 \left( k_3 P_1 - k_1 P_3 \right) \mathrm{\cos} \lef... ...} \left( k_2 x_2 \right) \mathrm{\cos} \left( k_3 x_3 \right), \end{displaymath}

\begin{displaymath}B_3 = - 8 \left( k_1 P_2 - k_2 P_1 \right) \mathrm{\cos} \lef... ... \left( k_2 x_2 \right) \mathrm{\sin} \left( k_3 x_3 \right) . \end{displaymath}

When the oven is hot, we can expect that it will contain electromagnetic radiation in these possible modes of oscillation. Let's now consider a sum of the above possible modes of electromagnetic radiation in the oven for all the possible values of $k$, as above, and the two independent values 0 and $- \frac{\pi}{2}$ of $\theta$. There is an independent polarization vector $P$ for each pair $\left( k, \theta \right)$ of a possible value of $k$ and one of the two independent values 0 and $- \frac{\pi}{2}$ of $\theta$, and I'll write this as $P \left( n, \theta \right)$, where $n_a$ are whole numbers $\geq 0$ such that $k_a = \frac{\pi n_a}{L_a}$, for $a = 1, 2, 3$. The symbol $\geq$ means, "greater than or equal to." The polarization vector $P \left( n, \theta \right)$ satisfies $\sum_a n_a P_a \left( n, \theta \right) = 0$. The 1 component of the electric field strength $E$ is now:

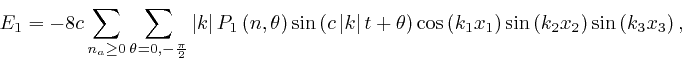
\begin{displaymath}E_1 = - 8 c \sum_{n_a \geq 0} \sum_{\theta = 0, - \frac{\pi}{... ...} \left( k_2 x_2 \right) \mathrm{\sin} \left( k_3 x_3 \right), \end{displaymath}

where $\sum_{n_a \geq 0}$ means $\sum_{n_1 \geq 0} \sum_{n_2 \geq 0} \sum_{n_3 \geq 0}$, and the other components of $E$ and the components of $B$ are now analogous sums of the components above.

From the gauge-invariant formula for the Hamiltonian for a collection of electrically charged point particles moving slowly compared to the speed of light in a vacuum, plus electric and magnetic fields, which we found in the previous post, here, the energy of the electromagnetic fields in the oven involves the integrals over the volume of the oven of the squares of the components of $E$ and $B$. To calculate the contribution of $E^2_1$, where $E_1$ is equal to a sum over the independent modes as above, it is convenient to use independent dummy indexes $n, \theta$ and $n', \theta'$ for each of the two factors of $E_1$, so that $E^2_1$ can be written as:

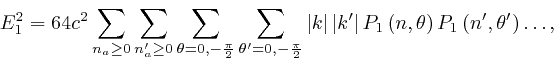
\begin{displaymath}E^2_1 = 64 c^2 \sum_{n_a \geq 0} \sum_{n'_a \geq 0} \sum_{\th... ...eft( n, \theta \right) P_1 \left( n', \theta' \right) \ldots, \end{displaymath}

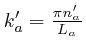where $\ldots$ stand for the remaining factors, and $k'_a = \frac{\pi n'_a}{L_a}$, for $a = 1, 2, 3$.

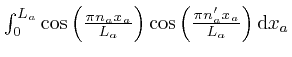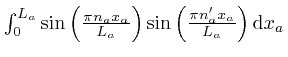Considering a term in the above sum with specific values of $n$, $n'$, $\theta$, and $\theta'$, the integral over the volume of the oven factorizes into a product of integrals of the form $\int_0^{L_a} \mathrm{\cos} \left( \frac{\pi n_a x_a}{L_a} \right) \mathrm{\cos} \left( \frac{\pi n'_a x_a}{L_a} \right) \mathrm{d} x_a$ or $\int_0^{L_a} \mathrm{\sin} \left( \frac{\pi n_a x_a}{L_a} \right) \mathrm{\sin} \left( \frac{\pi n'_a x_a}{L_a} \right) \mathrm{d} x_a$, there being one such factor for each of the three possible values of $a$. From the result we found above, and the observations above, we have:

\begin{displaymath}\mathrm{\cos} \left( y_1 \right) \mathrm{\cos} \left( y_2 \ri... ...y_2 \right) + \mathrm{\cos} \left( y_1 + y_2 \right) \right), \end{displaymath}

\begin{displaymath}\mathrm{\sin} \left( y_1 \right) \mathrm{\sin} \left( y_2 \ri... ...y_2 \right) - \mathrm{\cos} \left( y_1 + y_2 \right) \right), \end{displaymath}

for all $y_1$ and all $y_2$. Thus we have:

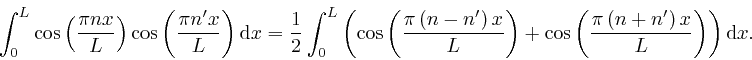
\begin{displaymath}\int_0^L \mathrm{\cos} \left( \frac{\pi nx}{L} \right) \mathr... ...\pi \left( n + n' \right) x}{L} \right) \right) \mathrm{d} x. \end{displaymath}

We now observe that if $b$ is a fixed number, and $f$ is a quantity that depends smoothly on a quantity $y$, so in the terminology of the previous post, here, $f$ is a smooth function of $y$, then:

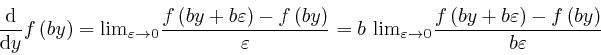
\begin{displaymath}\frac{\mathrm{d}}{\mathrm{d} y} f \left( by \right) = \mathr... ...+ b \varepsilon \right) - f \left( by \right)}{b \varepsilon} \end{displaymath}

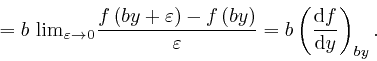
\begin{displaymath}= b\,\, \mathrm{\lim}_{\varepsilon \rightarrow 0} \frac{f \le... ...} = b \left( \frac{\mathrm{d} f}{\mathrm{d} y} \right)_{by} . \end{displaymath}

So from the result we found in the first post in the series, here, we have:

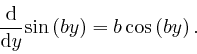
\begin{displaymath}\frac{\mathrm{d}}{\mathrm{d} y} \mathrm{\sin} \left( by \right) = b\, \mathrm{\cos} \left( by \right) . \end{displaymath}

Thus from the result we found in the first post in the series, here, that the integral of the rate of change of a quantity is equal to the net change of that quantity, we have:

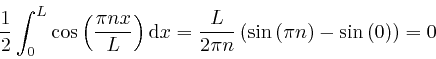
\begin{displaymath}\frac{1}{2} \int_0^L \mathrm{\cos} \left( \frac{\pi nx}{L} \r... ...t( \pi n \right) - \mathrm{\sin} \left( 0 \right) \right) = 0 \end{displaymath}

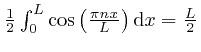if $n$ is a whole number $\neq 0$, while for $n = 0$ we have $\frac{1}{2} \int_0^L \mathrm{\cos} \left( \frac{\pi nx}{L} \right) \mathrm{d} x = \frac{L}{2}$. Thus from the result above, we find that for whole numbers $n \geq 0$ and $n' \geq 0$:

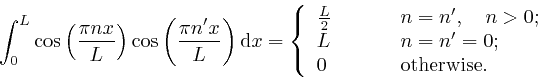
\begin{displaymath}\int_0^L \mathrm{\cos} \left( \frac{\pi nx}{L} \right) \mathr... ...0 \hspace{1.3cm} \mathrm{{{otherwise}}} . \end{array} \right. \end{displaymath}

And similarly:

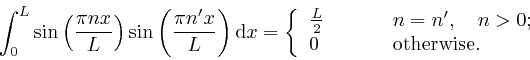
\begin{displaymath}\int_0^L \mathrm{\sin} \left( \frac{\pi nx}{L} \right) \mathr... ...0 \hspace{1.3cm} \mathrm{{{otherwise}}} . \end{array} \right. \end{displaymath}

Thus after doing the integral over the volume of the oven, the contribution from $E^2_1$ to the gauge-invariant formula for the total energy, $H_{\mathrm{g.i.}}$, as in the previous post, here, is:

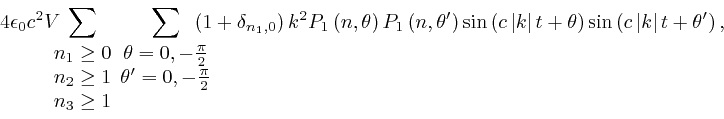
\begin{displaymath}4 \epsilon_0 c^2 V \hspace{-1.0em} \sum_{{\scriptstyle{\begin... ...{\sin} \left( c \left\vert k \right\vert t + \theta' \right), \end{displaymath}

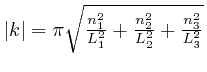where $V$ now represents the volume $L_1 L_2 L_3$ of the oven, and $\left\vert k \right\vert = \pi \sqrt{\frac{n^2_1}{L^2_1} + \frac{n^2_2}{L^2_2} + \frac{n^2_3}{L^2_3}}$. The expression $\delta_{n_1,0}$ is 1 if $n_1 = 0$ and 0 otherwise, in accordance with the definition of the Kronecker delta, in the first post in the series, here. And in the same way, we find that when $B^2_1$ is expressed as a sum over $n, \theta, n'$, and $\theta'$, analogous to the expression for $E^2_1$ above, the contributions from $B^2_1$ to $H_{\mathrm{g.i.}}$ with $n \neq n'$ give 0 after doing the integral over the volume of the oven.

We'll focus now on the contributions of modes with $n_a > 0$ for all $a = 1, 2, 3$. From the formula above and the analogous formulae for the contributions from $E^2_2$ and $E^2_3$, the sum of the contributions from $E^2_1$, $E^2_2$, and $E^2_3$, for the modes with $n_a > 0$ for all $a = 1, 2, 3$, is:

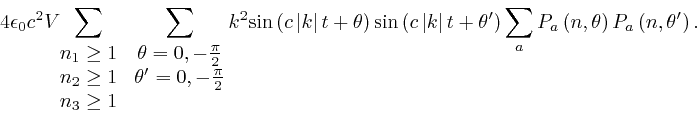
\begin{displaymath}4 \epsilon_0 c^2 V \hspace{-0.7em} \sum_{{\scriptstyle{\begin... ... P_a \left( n, \theta \right) P_a \left( n, \theta' \right) . \end{displaymath}

And from the formulae for the components of $B$, above, the sum of the contributions from $B^2_1$, $B^2_2$, and $B^2_3$, to $H_{\mathrm{g.i.}}$, as in the previous post, here, for the modes with $n_a > 0$ for all $a = 1, 2, 3$, is:

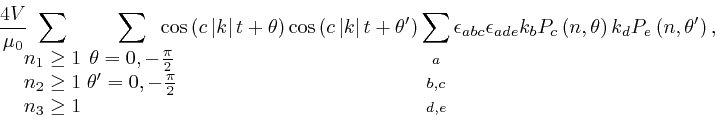
\begin{displaymath}\frac{4 V}{\mu_0} \hspace{-0.9em} \sum_{{\scriptstyle{\begin{... ...c \left( n, \theta \right) k_d P_e \left( n, \theta' \right), \end{displaymath}

since, for example, $k_2 P_3 - k_3 P_2 = \sum_{b, c} \epsilon_{1 b c} k_b P_c$, from the definition of the antisymmetric tensor $\epsilon_{a b c}$, in the third post in the series, here. From the formula we found in the third post in the series, here, with the indexes $a$ and $b$ rewritten as $b$ and $c$, and the dummy index $c$ rewritten as $a$, and the property of the Kronecker delta we observed in the third post in the series, here, the above expression is equal to:

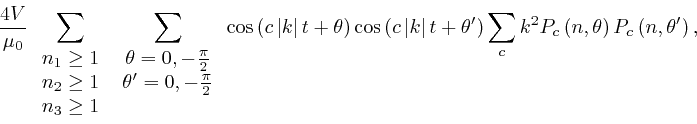
\begin{displaymath}\frac{4 V}{\mu_0} \sum_{{\scriptstyle{\begin{array}{c} n_1 \... ...2 P_c \left( n, \theta \right) P_c \left( n, \theta' \right), \end{displaymath}

since $\sum_b k_b P_b \left( n, \theta' \right) = \sum_c k_c P_c \left( n, \theta \right) = 0$.

We found in the third post in the series, here, that $c$, the speed of light in a vacuum, is equal to $\frac{1}{\sqrt{\epsilon_0 \mu_0}}$, so the factor $4 \epsilon_0 c^2 V$ in the contribution from $E^2$ is equal to the factor $\frac{4 V}{\mu_0}$ in the contribution from $B^2$. Thus for each $n$, our observation above implies that the total contribution from terms where $\theta = 0$ and $\theta' = - \frac{\pi}{2}$, or vice versa, is proportional to:

\begin{displaymath}\mathrm{\sin} \left( c \left\vert k \right\vert t \right) \ma... ...} \left( c \left\vert k \right\vert t - \frac{\pi}{2} \right) \end{displaymath}

\begin{displaymath}= \mathrm{\sin} \left( c \left\vert k \right\vert t \right) \... ...ght) \mathrm{\sin} \left( c \left\vert k \right\vert t \right) \end{displaymath}

\begin{displaymath}= - \mathrm{\sin} \left( c \left\vert k \right\vert t \right)... ...ht) \mathrm{\sin} \left( c \left\vert k \right\vert t \right) \end{displaymath}

\begin{displaymath}= - \mathrm{\sin} \left( c \left\vert k \right\vert t \right)... ...ght) \mathrm{\sin} \left( c \left\vert k \right\vert t \right) \end{displaymath}

\begin{displaymath}= 0, \end{displaymath}

where at the second step I used the observation that $\mathrm{\sin} \left( y + \pi \right) = - \mathrm{\sin} \left( y \right)$ for all $y$, which follows from the definition of $\mathrm{\sin} \left( y \right)$, as in the first post in the series, here.

Thus since $\left( \mathrm{\cos} \left( y \right) \right)^2 + \left( \mathrm{\sin} \left( y \right) \right)^2 = 1$ for all $y$, the total contribution of the modes with $n_a > 0$ for all $a = 1, 2, 3$ to the energy of the electromagnetic radiation in the oven is:

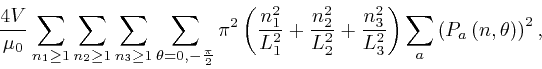
\begin{displaymath}\frac{4 V}{\mu_0} \sum_{n_1 \geq 1} \sum_{n_2 \geq 1} \sum_{n... ...\right) \sum_a \left( P_a \left( n, \theta \right) \right)^2, \end{displaymath}

where I used the formula for $\left\vert k \right\vert$ above.

We now observe that the arguments that led to the Boltzmann distribution, as in the second post in the series, here, for the most likely number of objects of a given type in a given position and momentum bin, when the range of possible positions and momenta of the microscopic objects in a system in thermal equilibrium at absolute temperature $T$ is divided up into tiny bins of equal size, can be adapted to the electromagnetic radiation subject to Maxwell's equations in a hot oven, for radiation of wavelengths very small compared to the dimensions $L_1$, $L_2$, and $L_3$ of the oven, in the following way.

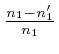We'll consider radiation modes whose wavelengths are sufficiently small compared to the dimensions of the oven that we can group the modes, described by their wave-number vector $n = \left( n_1, n_2, n_3 \right)$ and $\theta = 0$ or $- \frac{\pi}{2}$, into "types" of similar $n$ and equal $\theta$, such that the number of modes of each type is large compared to 1, and the relative differences $\frac{n_1 - n'_1}{n_1}$, $\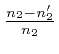frac{n_2 - n'_2}{n_2}$, and $\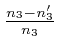frac{n_3 - n'_3}{n_3}$, between the wave-number vectors $n$ and $n'$ of any two modes of the same type are small compared to 1. For example for infra-red radiation of wavelength about $10^{- 6}$ metres in an oven of size about a metre cubed, we can assume that $n_1$, $n_2$, and $n_3$ are all at least about $10^6$, and divide up the range of each $n_a \geq 10^6$ into ranges $10^6$ to $10^6 + 10^3 - 1$; $10^6 + 10^3$ to $10^6 + 2 \times 10^3 - 1$; and so on, and say that two wave-number vectors $n$ and $n'$ are of the same type if $n_a$ is in the same range as $n'_a$, for $a = 1, 2$, and 3. 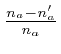Then the number of wave-number vectors of each type is $10^9$, and for $n$ and $n'$ of the same type, $\frac{n_a - n'_a}{n_a}$ is $\leq 10^{- 3}$, for $a = 1, 2$, and 3. This is consistent with the definition of the type of an object that I gave in the second post in the series, here, in the course of the derivation of the Boltzmann distribution.

Looking back at the derivation of the Boltzmann distribution, in the second post in the series, starting here, we observe that it depended on the assumption that the number of objects of each type is very large compared to 1, and that requirement will be satisfied for the radiation modes in the oven if we regard the modes of wave-number vector $n$ such that $n_a \geq 10^6$ for $a = 1, 2$, and 3 as "objects", and classify them into types as I just described.

The derivation of the Boltzmann distribution also depended on the conserved total energy being equal to the sum of the energies of the individual objects, so that the range of possible positions and momenta of an object could be divided into very small bins, such that the conserved total energy $E$ is to a very good approximation equal to a sum $\sum_j \sum_s n_{j s} E_{j s}$, as in the second post in the series, here, where $n_{j s}$ is the number of objects of type $j$ in bin $s$, and $E_{j s}$ is the energy of an object of type $j$ at the centre of bin $s$. However the derivation did not depend on any particular details of how $E_{j s}$ depends on the type of object $j$ or the position and momentum of an object at the centre of bin $s$, and it did not depend on the numbers associated with an object, that determine the contribution of that object to the total energy $E$, being the position and momentum coordinates of the object, as opposed to some other quantities associated to the object that determine its contribution to $E$.

Thus from the formula above for the contribution of the modes with $n_a > 0$ for all $a = 1, 2, 3$ to the energy of the electromagnetic radiation in the oven, which shows that the energy is the sum of a contribution from each mode, the argument works equally well if we regard the modes of wave-number vector $n$ such that $n_a \geq 10^6$ for $a = 1, 2$, and 3 as objects, and classify them into types as I described above, where the variable quantities associated with each object, that determine the contribution of that object to $E$, are the components of the polarization vector $P_a \left( n, \theta \right)$ of that mode. Two of the three components of $P_a \left( n, \theta \right)$ can vary independently for each mode, due to the restriction that $\sum_{a = 1}^3 n_a P_a \left( n, \theta \right) = 0$, as above.

The derivation of the Boltzmann distribution depended on the range of possible values of the position and momentum coordinates of an object being divided into bins of equal size, but although I used the same bins, for convenience, for each different type of object, the derivation did not depend on that, and neither the derivation nor the result, as in the second post in the series, here, depended on the actual sizes of the bins, other than through the requirements that they be small enough that the energies of all the objects of type $j$ in bin $s$ are equal to $E_{j s}$ to a good accuracy, and that they be large enough, or that the total number $m_j$ of objects of type $j$ be large enough, that the total number of objects in each bin, or at least, in the bins with the largest numbers of objects of type $j$, should be large compared to 1. The derivation of the formula $f_{j s} = \frac{n_{j s}}{N} = \mathrm{e}^{- \beta E_{j s} - \gamma_j}$, in the second post in the series, starting here, was carried out separately for each different type of object $j$, and the value of $\mathrm{e}^{\gamma_j}$ for each different type of object, as in the formula in the second post in the series, here, or in the example of the ideal gas, which we studied in the second post in the series, starting here, automatically compensates for any change of the bin size for each different type of object.

From the formula above, the contribution of a mode the energy of the electromagnetic radiation in the oven is proportional to the sum of the squares of the components of the polarization vector of the mode, so from the analogy to the kinetic energy of a particle, which is proportional to the sum of the squares of the components of the momentum vector of the particle, I shall assume that it is the range of possible polarization vectors of a mode that should be divided into equal size bins. The modes are grouped into types of approximately equal wave-number vector $n$ and equal $\theta$ as above, and for a type whose wave-number is $n$, we'll choose two vectors $u_1$ and $u_2$ of length 1 that are perpendicular to $n$ and perpendicular to each other. We'll represent the components of the polarization vector $P_a \left( n, \theta \right)$ in the directions $u_1$ and $u_2$ by $P'_1 \left( n, \theta \right)$ and $P'_2 \left( n, \theta \right)$, so from the formula in the third post in the series, here:

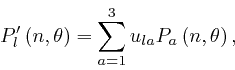
\begin{displaymath}P'_l \left( n, \theta \right) = \sum_{a = 1}^3 u_{l a} P_a \left( n, \theta \right), \end{displaymath}

for $l = 1, 2$. The mutually perpendicular vectors $\frac{n}{\left\vert n \right\vert}$, $u_1$, and $u_2$ are the vectors of length 1 in the coordinate directions of an alternative system of Cartesian coordinates, so by Pythagoras:

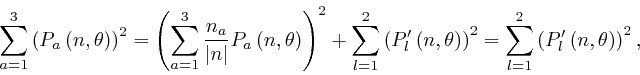
\begin{displaymath}\sum_{a = 1}^3 \left( P_a \left( n, \theta \right) \right)^2 ... ...\sum_{l = 1}^2 \left( P'_l \left( n, \theta \right) \right)^2, \end{displaymath}

since $\sum_{a = 1}^3 n_a P_a \left( n, \theta \right) = 0$.

Thus from the formula above, the energy of a mode of type $\left( n, \theta \right)$ with independent polarization vector components $P'_1$ and $P'_2$ is:

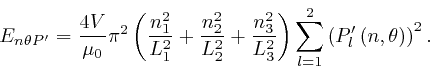
\begin{displaymath}E_{n \theta P'} = \frac{4 V}{\mu_0} \pi^2 \left( \frac{n^2_1}... ...um_{l = 1}^2 \left( P'_l \left( n, \theta \right) \right)^2 . \end{displaymath}

So in a similar manner to the calculation for an ideal gas, in the second post in the series, starting here, we find from the result in the second post in the series, here, that the most likely number of modes of type $\left( n, \theta \right)$ in a polarization bin with edge sizes $\mathrm{d} P'_1$ and $\mathrm{d} P'_2$ is:

\begin{displaymath}n_{n \theta P'} = m_{n \theta} \frac{\mathrm{e}^{- \frac{E_{n... ...heta P''}}{\mathrm{k} T}} \mathrm{d} P''_1 \mathrm{d} P''_2}, \end{displaymath}

where $m_{n \theta}$ is the total number of modes of type $\left( n, \theta \right)$. From the result above, and the results we obtained in the second post in the series, here, and here, we find:

\begin{displaymath}\int \int \mathrm{e}^{- \frac{E_{n \theta P'}}{\mathrm{k} T}}... ...}{L^2_1} + \frac{n^2_2}{L^2_2} + \frac{n^2_3}{L^2_3} \right)}, \end{displaymath}

so:

\begin{displaymath}n_{n \theta P'} = \frac{4 \pi V}{\mu_0 \mathrm{k} T} \left( ... ... \theta P'}}{\mathrm{k} T}} \mathrm{d} P'_1 \mathrm{d} P'_2 . \end{displaymath}

In the same way as for the ideal gas example, in the second post in the series, here, we'll assume now that this most likely number of modes of type $\left( n, \theta \right)$ in each polarization bin is the actual number of modes in each polarization bin. So the total energy of the modes of type $\left( n, \theta \right)$ is:

\begin{displaymath}\frac{4 \pi V}{\mu_0 \mathrm{k} T} \left( \frac{n^2_1}{L^2_1}... ... \theta P'}}{\mathrm{k} T}} \mathrm{d} P'_1 \mathrm{d} P'_2 = \end{displaymath}

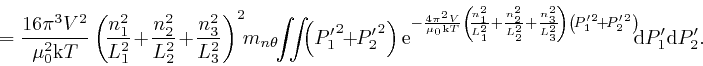
\begin{displaymath}= \frac{16 \pi^3 V^2}{\mu^2_0 \mathrm{k} T} \left( \! \frac{n... ...+ \! {P'_2}^2 \right)} \!\! \mathrm{d} P'_1 \mathrm{d} P'_2 . \end{displaymath}

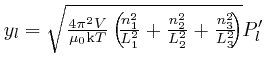From the result in the second post in the series, here, with $y_l = \sqrt{\frac{4 \pi^2 V}{\mu_0 \mathrm{k} T} \left( \!\! \frac{n^2_1}{L^2_1} + \frac{n^2_2}{L^2_2} + \frac{n^2_3}{L^2_3} \!\! \right)} P'_l$, $l = 1, 2$, this is equal to:

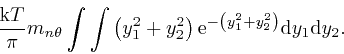
\begin{displaymath}\frac{\mathrm{k} T}{\pi} m_{n \theta} \int \int \left( y^2_1 ... ...\left( y^2_1 + y^2_2 \right)} \mathrm{d} y_1 \mathrm{d} y_2 . \end{displaymath}

And from the calculation in the second post in the series, starting here, this is equal to:

\begin{displaymath}\mathrm{k} Tm_{n \theta} . \end{displaymath}

Thus in thermal equilibrium at absolute temperature $T$, each of the $m_{n \theta}$ modes of type $\left( n, \theta \right)$ has energy $\mathrm{k} T$. Since this is independent of $n$ and $\theta$, we thus find that for every mode $\left( n, \theta \right)$ for which all three components of $n$ are sufficiently large, the energy of that mode, in thermal equilibrium at absolute temperature $T$, is $\mathrm{k} T$. From the discussion above, this applies, in particular, for electromagnetic radiation of infra-red and all shorter wavelengths in an oven of size about a metre cubed or larger, for almost all directions of the wave-number vector $n$.

Thus since there is no upper limit to the size of the components of the wave-number vector $n$, we have arrived at a result in contradiction with everyday experience: if the absolute temperature $T$ of the oven is greater than 0, then the energy of the electromagnetic radiation in the oven is infinite, because there are an infinite number of modes, each of which has energy $\mathrm{k} T$.

At the end of the nineteenth century, the actual energy of the electromagnetic radiation in different frequency ranges in hot ovens was measured by Otto Lummer, Ferdinand Kurlbaum, and Heinrich Rubens. From the formulae for the electric and magnetic fields in the waves, above, the angular frequency $\omega$, where $\omega$ is the Greek letter omega, which is $2 \pi$ times the number of cycles per unit time, is $\omega = c \left\vert k \right\vert$, where the wavevector $k$ is $k_a = \frac{\pi n_a}{L_a}$, from above, and the speed of light is $c = \frac{1}{\sqrt{\epsilon_0 \mu_0}}$, from the third post in the series, here. Each wave-number vector $n$ corresponds to 2 modes, one for each of the two values 0 and $- \frac{\pi}{2}$ of $\theta$, so the number of modes per unit volume in the space of wavevectors is $\frac{2 L_1 L_2 L_3}{\pi^3} = \frac{2 V}{\pi^3}$. Each component of $k$ is $> 0$, so from the value we found in the third post in the series, here, for the area of a sphere of radius 1, the total number of modes whose wavevector magnitude lies in the range from $\left\vert k \right\vert$ to $\left\vert k \right\vert + \mathrm{d} \left\vert k \right\vert$ is:

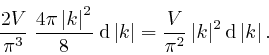
\begin{displaymath}\frac{2 V}{\pi^3} \: \frac{4 \pi \left\vert k \right\vert^2}{... ...ft\vert k \right\vert^2 \mathrm{d} \left\vert k \right\vert . \end{displaymath}

Thus the total number of modes whose angular frequency lies in the range from $\omega$ to $\omega + \mathrm{d} \omega$ is $\frac{V}{\pi^2 c^3} \omega^2 \mathrm{d} \omega$, so since each of these modes has energy $\mathrm{k} T$ according to the result above, the total energy of electromagnetic radiation in the oven in modes whose angular frequency lies in the range from $\omega$ to $\omega + \mathrm{d} \omega$, according to the result above, is:

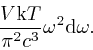
\begin{displaymath}\frac{V \mathrm{k} T}{\pi^2 c^3} \omega^2 \mathrm{d} \omega . \end{displaymath}

This is called the Rayleigh-Jeans law, after Lord Rayleigh and Sir James Jeans.

Max Planck discovered in 1900 that the measurements of Lummer, Kurlbaum, and Rubens are instead represented accurately by a formula:

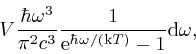
\begin{displaymath}V \frac{\hbar \omega^3}{\pi^2 c^3} \frac{1}{\mathrm{e}^{\hbar \omega / \left( \mathrm{k} T \right)} - 1} \mathrm{d} \omega, \end{displaymath}

where $\hbar$, which is pronounced "h bar", is a fundamental constant of nature that was previously unknown, whose value is:

\begin{displaymath}\hbar = 1.055 \times 10^{- 34} \hspace{0.4em} \mathrm{{{Joule}}} \hspace{0.4em} \mathrm{{{seconds}}}, \end{displaymath}

and $\mathrm{e} \simeq 2.718$ is Napier's number, as in the second post in the series, here.

From the formula in the second post in the series, here, the factor $\frac{1}{\mathrm{e}^{\hbar \omega / \left( \mathrm{k} T \right)} - 1}$ tends to $\frac{\mathrm{k} T}{\hbar \omega}$ as $\omega$ tends to 0, and is approximately equal to $\frac{\mathrm{k} T}{\hbar \omega}$ for all $\omega$ such that $\hbar \omega < \mathrm{k} T$, so the Rayleigh-Jeans law, as above, is approximately valid for all $\omega$ such that $\hbar \omega < \mathrm{k} T$, and becomes accurately valid when $\hbar \omega$ is substantially smaller than $\mathrm{k} T$. However at $\omega$ such that $\hbar \omega \simeq 2.821 \mathrm{k} T$, the energy in modes whose angular frequency lies in the range from $\omega$ to $\omega + \mathrm{d} \omega$ stops growing with $\omega$ as predicted by the Rayleigh-Jeans law, and at larger $\omega$ it decreases very rapidly with increasing $\omega$, in complete contradiction with the Rayleigh-Jeans law.

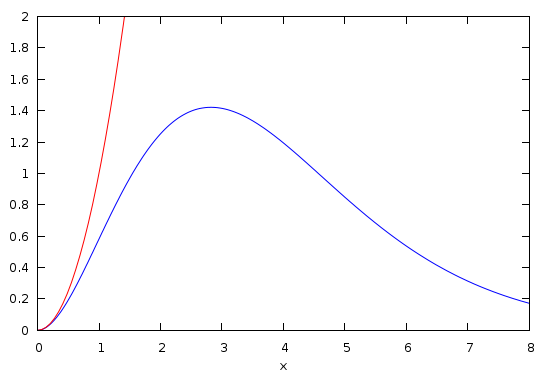
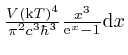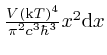If we define $x = \frac{\hbar \omega}{\mathrm{k} T}$, then the Planck law, above, becomes $\frac{V \left( \mathrm{k} T \right)^4}{\pi^2 c^3 \hbar^3} \frac{x^3}{\mathrm{e}^x - 1} \mathrm{d} x$, and the Rayleigh-Jeans law, above, becomes $\frac{V \left( \mathrm{k} T \right)^4}{\pi^2 c^3 \hbar^3} x^2 \mathrm{d} x$. This graph shows the Planck factor, $\frac{x^3}{\mathrm{e}^x - 1}$, which is in agreement with observation, plotted in blue, and the Rayleigh-Jeans factor, $x^2$, plotted in red. We see that the Rayleigh-Jeans factor is already too large by about a factor of 2 at $x = 1$, and only agrees well with the correct Planck factor for $x$ less than about 0.4.

The quantity $2 \pi \hbar$ is known as Planck's constant. The dimensions of $\hbar$ are energy times time, which are the dimensions of de Maupertuis's action. Planck suggested that energy could be transferred between the oven walls and the electromagnetic radiation of frequency $\omega$ in the oven only in whole number multiples of a basic amount $\hbar \omega$. This was the start of the discoveries that led to Dirac-Feynman-Berezin sums, and which made possible, among other things, the design and construction of the electronic device on which you are reading this blog post.

In the next post in this series, Dirac-Feynman sums, we'll take a first look at a special case of Dirac-Feynman-Berezin sums, which I'll call Dirac-Feynman sums. We'll see that Dirac-Feynman sums lead to de Maupertuis's principle, Newton's laws, and Maxwell's equations, when the energies involved are large compared to Planck's basic amount $\hbar \omega$, but lead to essential corrections when the energies involved are comparable in size to $\hbar \omega$, or smaller than $\hbar \omega$. In particular, Dirac-Feynman sums correct the Rayleigh-Jeans law to the Planck law, when the Boltzmann energy $\mathrm{k} T$ is comparable to or smaller than the Planck energy $\hbar \omega$.

The software on this website is licensed for use under the Free Software Foundation General Public License.

Page last updated 4 May 2023. Copyright (c) Chris Austin 1997 - 2023. Privacy policy